Giải mục 1 trang 37, 38, 39 SGK Toán 11 tập 2 - Chân trời sáng tạo — Không quảng cáo

Hoạt động 1

Quãng đường rơi tự do của một vật được biểu diễn bởi công thức $s\left( t \right) = 4,9{t^2}$ với $t$ là thời gian tính bằng giây và $s$ tính bằng mét.

Vận tốc trung bình của chuyển động này trên khoảng thời gian $\left[ {5;t} \right]$ hoặc $\left[ {t;5} \right]$ được tính bằng công thức $\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}$.

a) Hoàn thiện bảng sau về vận tốc trung bình trong những khoảng thời gian khác nhau. Nêu nhận xét về $\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}$ khi $t$ càng gần 5.

b) Giới hạn $\mathop {\lim }\limits_{t \to 5} \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}$ được gọi là vận tốc tức thời của chuyển động tại thời điểm ${t_0} = 5$. Tính giá trị này.

c) Tính giới hạn $\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}}$ để xác định vận tốc tức thời của chuyển động tại thời điểm ${t_0}$ nào đó trong quá trình rơi của vật.

Phương pháp giải:

a) Thay vào công thức $\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}$.

b) c) Sử dụng các quy tắc tính giới hạn.

Lời giải chi tiết:

a)

$\begin{array}{l}\begin{array}{*{20}{l}}{\left[ {5;5,1} \right]}\end{array}:t = 5,1 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{1^2} - 4,{{9.5}^2}}}{{5,1 - 5}} = 49,49\\\begin{array}{*{20}{l}}{\left[ {5;5,05} \right]}\end{array}:t = 5,05 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{05}^2} - 4,{{9.5}^2}}}{{5,05 - 5}} = 49,245\\\begin{array}{*{20}{l}}{\left[ {5;5,01} \right]}\end{array}:t = 5,01 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{01}^2} - 4,{{9.5}^2}}}{{5,01 - 5}} = 49,049\\\begin{array}{*{20}{l}}{\left[ {5;5,001} \right]}\end{array}:t = 5,001 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{001}^2} - 4,{{9.5}^2}}}{{5,001 - 5}} = 49,0049\\\begin{array}{*{20}{l}}{\left[ {4,999;5} \right]}\end{array}:t = 4,999 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{999}^2} - 4,{{9.5}^2}}}{{4,999 - 5}} = 48,9951\\\begin{array}{*{20}{l}}{\left[ {4,99;5} \right]}\end{array}:t = 4,99 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{99}^2} - 4,{{9.5}^2}}}{{4,99 - 5}} = 48,951\end{array}$

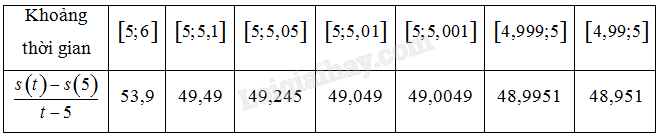
Ta thấy: $\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}$ càng gần 49 khi $t$ càng gần 5.

b)

$\begin{array}{l}\mathop {\lim }\limits_{t \to 5} \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,{{9.5}^2}}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - {5^2}} \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - 5} \right)\left( {t + 5} \right)}}{{t - 5}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + 5} \right) = 4,9\left( {5 + 5} \right) = 49\end{array}$

c)

$\begin{array}{l}\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,9.t_0^2}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - t_0^2} \right)}}{{t - t_0^2}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - {t_0}} \right)\left( {t + {t_0}} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + {t_0}} \right) = 4,9\left( {{t_0} + {t_0}} \right) = 9,8{t_0}\end{array}$

Thực hành 1

Tính đạo hàm của hảm số $f\left( x \right) = {x^3}$.

Phương pháp giải:

Tính giới hạn $f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}$.

Lời giải chi tiết:

Với bất kì ${x_0} \in \mathbb{R}$, ta có:

$\begin{array}{l}f\prime ({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - {x_0}^3}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x.{x_0} + {x_0}^2} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x.{x_0} + {x_0}^2} \right) = {x^2} + {x_0}.{x_0} + {x_0}^2 = 3{x_0}^2\end{array}$

Vậy $f'\left( x \right) = {\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}$ trên $\mathbb{R}$.

Vận dụng

Với tình huống trong Hoạt động mở đầu, hãy tính vận tốc tức thời của chuyển động lúc $t = 2$.

Phương pháp giải:

Tính $v\left( 2 \right) = s'\left( 2 \right)$ với $s\left( t \right) = 4,9{t^2}$.

Lời giải chi tiết:

Với bất kì ${t_0} \in \mathbb{R}$, ta có:

$s'\left( {{t_0}} \right) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}} = 9,8{t_0}$

Vậy $s'\left( t \right) = 9,8t$ trên $\mathbb{R}$.

Vậy vận tốc tức thời của chuyển động lúc $t = 2$ là: $v\left( 2 \right) = s'\left( 2 \right) = 9,8.2 = 19,6\left( {m/s} \right)$