Giải mục 2 trang 114, 115 SGK Toán 11 tập 1 - Kết nối tri thức
Cho hàm số (fleft( x right) = 1 + frac{2}{{x - 1}}) có đồ thị như Hình 5.4.Giả sử (left( {{x_n}} right)) là dãy số sao cho ({x_n} > 1,;{x_n} to ; + infty ). Tính (fleft( {{x_n}} right)) và (mathop {{rm{lim}}}limits_{n to + infty } fleft( {{x_n}} right))
HĐ 3
Cho hàm số \(f\left( x \right) = 1 + \frac{2}{{x - 1}}\) có đồ thị như Hình 5.4.
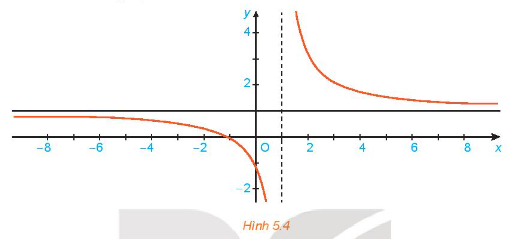
Giả sử \(\left( {{x_n}} \right)\) là dãy số sao cho \({x_n} > 1,\;{x_n} \to \; + \infty \). Tính \(f\left( {{x_n}} \right)\) và \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } f\left( {{x_n}} \right)\).
Phương pháp giải:
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Ta có hàm số \(f\left( x \right)\) có giới hạn là số L khi \(x \to + \infty \) nếu dãy số \(\left( {{x_n}} \right)\) bất kỳ, \({x_n} > a\) và \({x_n} \to + \infty \), ta có \(f\left( {{x_n}} \right) \to L,\) kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L\;\)hay \(f\left( x \right) \to L\) khi \(x \to + \infty \)
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( { - \infty ;b} \right)\). Ta có hàm số \(f\left( x \right)\) có giới hạn là số L khi \(x \to - \infty \) nếu dãy số \(\left( {{x_n}} \right)\) bất kỳ, \({x_n} < b\) và \({x_n} \to - \infty \), ta có \(f\left( {{x_n}} \right) \to L,\) kí hiệu \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = L\;\)hay \(f\left( x \right) \to L\) khi \(x \to - \infty \).
Lời giải chi tiết:
\(f\left( {{x_n}} \right) = 1 + \frac{2}{{{x_n} - 1}}\).
\(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right) = \mathop {\lim }\limits_{n \to + \infty } \left( {1 + \frac{2}{{{x_n} - 1}}} \right) = 1\).
LT 3
Tính: \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 2} }}{{x + 1}}\).
Phương pháp giải:
\(a\sqrt b = \left\{ {\begin{array}{*{20}{c}}{\sqrt {{a^2}b} \;\;\;\;\;\;\;\;\;a \ge 0}\\{ - \sqrt {{a^2}b} \;\;\;\;\;a < 0}\end{array}} \right.\).
Lời giải chi tiết:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {{x^2} + 2} }}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left| x \right|\sqrt {1 + \frac{2}{{{x^2}}}} }}{{x + 1}}\\ = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\sqrt {1 + \frac{2}{{{x^2}}}} }}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {1 + \frac{2}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\end{array}\)
VD
Cho tam giác vuông OAB với \(A = \left( {a;0} \right)\) và \(B = \left( {0;1} \right)\) như Hình 5.5. Đường cao OH có độ dài là h.
a) Tính h theo a,.
b) Khi điểm A dịch chuyển về O , điểm H thay đổi thế nào? Tại sao?
c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox , điểm H thay đổi thế nào? Tại sao?
Phương pháp giải:
Áp dụng định lý Pytago để tính h theo a.
Tính giới hạn.
Lời giải chi tiết:
a) Ta có: \(AB = \sqrt {{a^2} + {1^1}} ,\;\;\;AB \times OH = OB \times OA\)
\( \Rightarrow h \times \sqrt {{a^2} + {1^2}} = a \Rightarrow h = \frac{a}{{\sqrt {{a^2} + {1^2}} }}\)
b) \(\mathop {\lim }\limits_{a \to 0} \frac{a}{{\sqrt {{a^2} + {1^2}\;} }} = \mathop {\lim }\limits_{a \to 0} \frac{1}{{\sqrt {1 + \frac{1}{{{a^2}}}} }} = 0\)
Vì vậy khi A dịch chuyển về O thì điểm H dịch chuyển về gần A hơn, và h dần về 0
c) \(\mathop {\lim }\limits_{a \to + \infty } \frac{a}{{\sqrt {{a^2} + 1} }} = \mathop {\lim }\limits_{a \to + \infty } \frac{1}{{\sqrt {1 + \frac{1}{{{a^2}}}} }} = 1\)
Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H dịch chuyển về phía điểm B và h dần về 1.