Giải mục 2 trang 97, 98 SGK Toán 11 tập 1 - Kết nối tri thức
Quan sát Hình 4.56a và trả lời các câu hỏi sau: a) Hình chiếu O’ của điểm O có nằm trên đoạn A’C’ hay không? b) Hình chiếu của hai song cửa AB và CD như thế nào với nhau? c) Hình chiếu O’ của điểm O có phải là trung điểm của đoạn A’C’ hay
HĐ 2
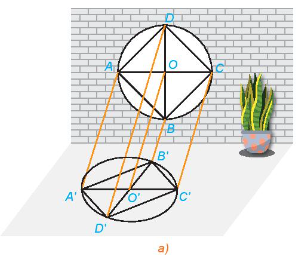
Quan sát Hình 4.56a và trả lời các câu hỏi sau:
a) Hình chiếu O’ của điểm O có nằm trên đoạn A’C’ hay không?
b) Hình chiếu của hai song cửa AB và CD như thế nào với nhau?
c) Hình chiếu O’ của điểm O có phải là trung điểm của đoạn A’C’ hay không?
Phương pháp giải:
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
a) Hình chiếu O’ của điểm O nằm trên đoạn A’C’.
b) Hình chiếu song song của AB và CD song song với AB và CD.
c) Hình chiếu O’ của điểm O là trung điểm của đoạn A’C’.
LT 2
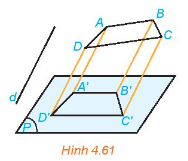
Chứng minh rằng hình chiếu song song của một hình thang là một hình thang (H.4.61).
Phương pháp giải:
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
Vì ABCD là hình thang nên AB // CD , do đó hình chiếu của AB là A'B' song song với hình chiếu của CD là C'D'.
Tứ giác A'B'C'D' có A'B' // C'D' nên nó là hình thang.
LT 3
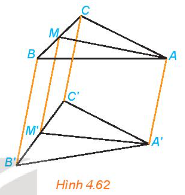
Một phép chiếu song song biến tam giác ABC thành tam giác A’B’C’, biến M thành M’ . Chứng minh rằng phép chiếu đó biến đường trung bình của tam giác ABC thành đường trung bình của tam giác A’B’C’.
Phương pháp giải:
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
MN là đường trung bình của tam giác AB C
Vì M là trung điểm của BC nên B, M, C thẳng hàng theo thứ tự đó và \(\frac{{BM}}{{MC}} = 1\).
Do vậy, B’, M’, C’ thẳng hàng theo thứ tự đó và \(\frac{{B'M'}}{{M'C'}} = 1\).
Tức M’ là trung điểm của B’C’.
Tương tự, N’ là trung điểm của A’C’.
Vậy M’N’ là đường trung bình của tam giác A’B’C’.