Giải mục 2 trang 120, 121 SGK Toán 11 tập 1 - Kết nối tri thức — Không quảng cáo

HĐ 2

Cho hai hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{2x\;,\;0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.$ và $g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x\;,0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.$với đồ thị tương ứng như Hình 5.7

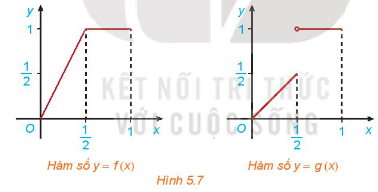
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm $x = \frac{1}{2}$ và nhận xét về sự khác nhau giữa hai đồ thị.

Phương pháp giải:

Hàm số $f\left( x \right)$ liên tục trên khoảng $\left( {a,b} \right)$ nếu nó liên tục tại mọi điểm thuộc khoảng này

Hàm số $f\left( x \right)$ liên tục trên đoạn $\left[ {a,b} \right]$ nếu nó liên tục trên khoảng $\left( {a,b} \right)$ và

$\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right),\;$ $\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)$

Lời giải chi tiết:

$\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} 2x = 1$

$\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} 1 = 1$

$f\left( {\frac{1}{2}} \right) = 1$

Vậy $f\left( x \right)$ liên tục tại $x = \frac{1}{2}$

$\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} x = \frac{1}{2}$

$\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} 1 = 1$

$g\left( {\frac{1}{2}} \right) = \frac{1}{2}$

Vậy $g\left( x \right)$ gián đoạn tại $x = \frac{1}{2}$

Đồ thị $f\left( x \right)$ liên tục trên đoạn $\left[ {0;1} \right],$ đồ thị $g\left( x \right)$ bị gián đoạn tại $x = \frac{1}{2}$

LT 2

Tìm các khoảng trên đó hàm số $f\left( x \right) = \frac{{{x^2} + 1}}{{x + 2}}$ liên tục.

Phương pháp giải:

Hàm phân thức liên tục trên tập xác định.

Lời giải chi tiết:

Tập xác định của $f\left( x \right)$ là $\left( { - \infty ;\; - 2} \right) \cup \left( { - 2;\; + \infty } \right)$

Vây hàm số $f\left( x \right)$ liên tục trên các khoảng $\left( { - \infty ; - 2} \right);\left( { - 2; + \infty } \right)$.