Giải mục 2 trang 62 SGK Toán 11 tập 2 - Cánh Diều — Không quảng cáo

Hoạt động 2

Cho hàm số y = f(x) có đồ thị (C), một điểm \({M_0}\) cố định thuộc (C) có hoành độ \({x_0}\). Với mỗi điểm M thuộc (C) khác \({M_0}\), kí hiệu \({x_M}\) là hoành độ của điểm M và \({k_M}\) là hệ số góc của cát tuyến \({M_0}M\). Giả sử tồn tại giới hạn hữu hạn \({k_0} = \mathop {\lim }\limits_{{x_M} \to {x_0}} {k_M}\). Khi đó, ta coi đường thẳng \({M_0}T\) đi qua \({M_0}\) và có hệ số góc là \({k_0}\) là ví trị giới hạn của cát tuyến \({M_0}M\) khi điểm M di chuyển dọc theo (C) dần tới \({M_0}\) . Đường thẳng \({M_0}T\)được gọi là tiếp tuyến của (C) tại điểm \({M_0}\), còn \({M_0}\) được gọi là tiếp điểm (Hình 3).

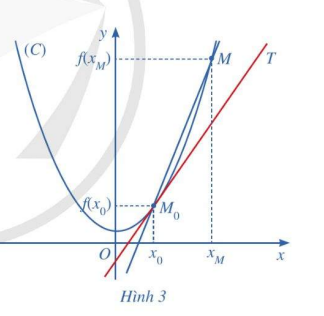
a)     Xác định hệ số góc \({k_0}\) của tiếp tuyến \({M_0}T\) theo \({x_0}\)

b)    Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\)

Phương pháp giải:

Áp dụng định nghĩa đạo hàm để làm bài

Lời giải chi tiết:

a)     \({k_0} = \mathop {\lim }\limits_{x \to {x_M}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}} = f'({x_0})\)

b)    Phương tình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\):

\(y = {k_0}(x - {x_0}) + {y_0}\)

Luyện tập – Vận dụng 3

Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{1}{x}\) tại điểm N (1; 1)

Phương pháp giải:

Dựa vào ví dụ 3 để làm

Lời giải chi tiết:

-         Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 có hệ số góc là:

\(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{x} - 1}}{{x - 1}} =  - 1\)

-         Phương trình tiếp tuyến của đồ thị tại điểm N(1; 1) là:

\(y =  - 1.\left( {x - 1} \right) + 1 =  - x + 1 + 1 =  - x + 2\)            \(\)