Giải mục 2 trang 51, 52, 53 SGK Toán 11 tập 2 - Cánh Diều — Không quảng cáo

HĐ 5

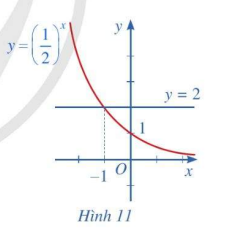
Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số mũ $y = {\left( {\frac{1}{2}} \right)^x}$. Từ đó, hãy tìm x sao cho ${\left( {\frac{1}{2}} \right)^x} > 2$

Phương pháp giải:

Dựa vào nhìn đồ thị để xét tính đồng biến nghịch biến

Lời giải chi tiết:

-         Hàm số $y = {\left( {\frac{1}{2}} \right)^x}$ nghịch biến trên toàn R

-         Dựa vào đồ thị ta thấy: ${\left( {\frac{1}{2}} \right)^x} > 2 \Leftrightarrow x >  - 1$

LT 5

Cho hai ví dụ về bất phương trình mũ cơ bản

Phương pháp giải:

Dựa vào định nghĩa bất phương trình mũ để xác định

Lời giải chi tiết:

Ví dụ:

+ ${3^x} = 9$

+ ${4^{x + 2}} = 16$

LT 6

Giải mỗi bất phương trình sau:

a)    ${7^{x + 3}} < 343$

b)    ${\left( {\frac{1}{4}} \right)^x} \ge 3$

Phương pháp giải:

Dựa vào ví dụ 10 để làm

Lời giải chi tiết:

a)    ${7^{x + 3}} < 343$

$\begin{array}{l} \Leftrightarrow x + 3 < {\log _7}343\\ \Leftrightarrow x + 3 < 3\\ \Leftrightarrow x < 0\end{array}$

Vậy tập nghiệm của bất phương trình là: $\left( { - \infty ;0} \right)$

b)    ${\left( {\frac{1}{4}} \right)^x} \ge 3$

$\Leftrightarrow x \le {\log _{\frac{1}{4}}}3$

Vậy tập nghiệm của bất phương trình là: $\left( { - \infty ;{{\log }_{\frac{1}{4}}}3} \right]$

HĐ 6

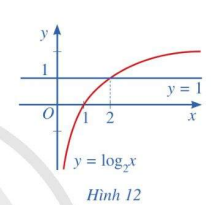
Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit $y = {\log _2}x$. Từ đó, hãy tìm x sao cho ${\log _2}x > 1$

Phương pháp giải:

Dựa vào nhìn đồ thị để xét tính đồng biến nghịch biến

Lời giải chi tiết:

-         Hàm số $y = {\log _2}x$ đồng biến trên tập xác định

-         Dựa vào đồ thị ta thấy: ${\log _2}x > 1 \Leftrightarrow x > 2$

LT 7

Cho hai ví dụ về bất phương trình logarit cơ bản

Phương pháp giải:

Dựa vào định nghĩa để làm

Lời giải chi tiết:

1. $\log x > 1$
2. ${\log _3}\left( {x + 1} \right) < 6$

LT 8

Giải mỗi bất phương trình sau:

a)    ${\log _3}x < 2$

b)    ${\log _{\frac{1}{4}}}\left( {x - 5} \right) \ge  - 2$

Phương pháp giải:

Dựa vào ví dụ 13 để làm

Lời giải chi tiết:

a)    ${\log _3}x < 2$

$\begin{array}{l} \Leftrightarrow 0 < x < {3^2}\\ \Leftrightarrow 0 < x < 9\end{array}$

Vậy tập nghiệm của bất phương trình là (0 ; 9)

b)    ${\log _{\frac{1}{4}}}\left( {x - 5} \right) \ge  - 2$

$\begin{array}{l} \Leftrightarrow 0 < x - 5 \le {\left( {\frac{1}{4}} \right)^{ - 2}}\\ \Leftrightarrow 5 < x \le 21\end{array}$

Vậy tập nghiệm của bất phương trình là $\left( {5;21} \right]$