Giải mục 2 trang 69, 70 SGK Toán 11 tập 1 - Cánh Diều
Cho hai hàm số (fleft( x right) = {x^2} - 1,gleft( x right) = x + 1.) a) Tính (mathop {lim }limits_{x to 1} fleft( x right)) và (mathop {lim }limits_{x to 1} gleft( x right).) b) Tính (mathop {lim }limits_{x to 1} left[ {fleft( x right) + gleft( x right)} right])và so sánh (mathop {lim }limits_{x to 1} fleft( x right) + mathop {lim }limits_{x to 1} gleft( x right).) c) Tính (mathop {lim }limits_{x to 1} left[ {fleft( x right) - gleft( x
Hoạt động 4
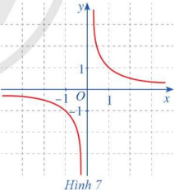
Cho hàm số \(f\left( x \right) = \frac{1}{x}\,\,\left( {x \ne 0} \right)\) có đồ thị như ở Hình 7 . Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
Phương pháp giải:
Quan sát đồ thị Hình 7 để trả lời câu hỏi.
Lời giải chi tiết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới 0.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới 0.
Luyện tập, vận dụng 4
Tính \(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 2}}{{4x - 5}}.\)
Phương pháp giải:
- Sử dụng \(\mathop {\lim }\limits_{x \to - \infty } \frac{c}{{{x^k}}} = 0;\mathop {\lim }\limits_{x \to - \infty } c = c\)
- Sử dụng các phép toán trên giới hạn.
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 2}}{{4x - 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {3 + \frac{2}{x}} \right)}}{{x\left( {4 - \frac{5}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{3 + \frac{2}{x}}}{{4 - \frac{5}{x}}} = \frac{{3 + 0}}{{4 - 0}} = \frac{3}{4}\)