Giải mục 2 trang 69, 70 SGK Toán 8 – Chân trời sáng tạo — Không quảng cáo

HĐ 2

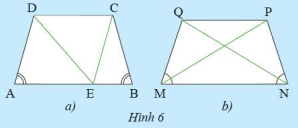
a) Cho hình thang cân $ABCD$ có hai đáy là $AB$ và $CD$ ( $AB > CD$ . Qua $C$ vẽ đường thẳng song song với $AD$ và cắt $AB$ tại $E$ (Hình 6a)

i) Tam giác $CEB$ là tam giác gì? Vì sao?

ii) So sánh $AD$ và $BC$

b) Cho hình thang cân $MNPQ$ có hai đáy là $MN$ và $PQ$ (Hình 6). So sánh $MP$ và $NQ$

Phương pháp giải:

Sử dụng kiến thức về góc tạo bởi hai đường thẳng song song (góc đồng vị) và định nghĩa hình thang cân để chỉ ra $\widehat {CEB} = \widehat {CBE}$ (do cùng bằng $\widehat {{\rm{DAE}}}$)

Lời giải chi tiết:

a) i) $ABCD$ là hình thang cân (gt)

$\Rightarrow \widehat A = \widehat B$ (1) và $DC$ // $AE$

Vì $AD\;{\rm{//}}\;CE$ (gt)

$\widehat A = \widehat {CEB}$ (cặp góc đồng vị)  (2)

Từ (1) và (2) suy ra: $\widehat {CEB} = \widehat B$

Suy ra $\Delta CEB$ là tam giác cân.

ii) $\Delta CEB$ cân tại $C$ (cmt)

Suy ra: $CE = BC$ (3)

Xét $\Delta ADE$ và $\Delta CED$ ta có:

$\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}$ ( $AD$ // $CE$ , cặp góc so le trong)

$DE$ chung

$\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}$ ( $CD$ // $AB$ , cặp góc so le trong)

Suy ra: $\Delta ADE = \Delta CED$ (g-c-g)

Suy ra: $AD = CE$ (4)

Từ (3) và (4) suy ra: $AD = BC$

b) Chứng minh tương tự như ý a) ta có: Hình thang cân $MNPQ$ có hai cạnh bên $MQ = NP$

Xét tam giác $\Delta MQP$ và $\Delta NPQ$ ta có:

$MQ = NP$ (cmt)

$\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}$ (do $MNPQ$ là hình thang cân)

$PQ$ chung

Suy ra: $\Delta MQP = \Delta NPQ$ (c-g-c)

$\Rightarrow MP = NQ$ (hai cạnh tương ứng)

TH 2

Tìm các đoạn thẳng bằng nhau trong hình thang cân $MNPQ$ có hai đáy $MN$ và $PQ$

Phương pháp giải:

Sử dụng tính chất của hình thang cân.

Lời giải chi tiết:

Vì $MNPQ$ là hình thang cân (gt)

Suy ra: $MP = NQ$ và $MQ = NP$

VD 3

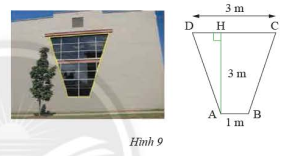
Một khung cửa sổ hình thang cân có chiều cao 3m, hai đáy là 3m và 1m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.

Phương pháp giải:

Kẻ đường cao $BK$

Sử dụng tính chất của hình thang cân

Lời giải chi tiết:

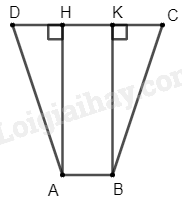
Kẻ đường cao $BK$

Suy ra $AH = BK$ và $AHKB$ là hình chữ nhật

Suy ra $HK = AB = 1$ cm

Vì $ABCD$ là hình thang cân (gt)

$\Rightarrow AC = BD$ và $AD = BC$ (tc)

Xét $\Delta AHD$ và $\Delta BKC$ ta có:

$\widehat {{\rm{AHD}}} = \widehat {{\rm{BKC}}} = 90^\circ$ (gt)

$\widehat D = \widehat C$ (định nghĩa hình thang cân)

$AD = BC$ (tính chất hình thang cân)

Suy ra: $\Delta AHD = \Delta BKC$ (ch – cgv)

Suy ra $DH = KC$ (hai cạnh tương ứng)

Suy ra $DH = KC = \frac{{CD - HK}}{2} = \frac{{3 - 1}}{2} = 1$ (cm)

Suy ra $HC = 2$ (cm)

Áp dụng định lý Pythagore vào tam giác vuông $AHD$ ta có:

$A{D^2} = D{H^2} + A{H^2} = {1^2} + {3^2} = 10$

Suy ra $AD = \sqrt {10}$ (cm)

Áp dụng định lý Pythagore vào tam giác vuông $ACH$ ta có:

$A{C^2} = A{H^2} + H{C^2} = {3^2} + {2^2} = 9 + 4 = 13$

$AC = \sqrt {13}$ (cm)

Vậy $AC = BD = \sqrt {13}$ cm; $AD = BC = \sqrt {10}$ cm