Giải mục 2 trang 63, 64, 65 SGK Toán 8 tập 2– Chân trời sáng tạo
a) Nếu
HĐ3
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) có đồng dạng với tam giác \(ABC\) không? Tỉ số đồng dạng là bao nhiêu?
b) Cho tam giác \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng \(k\) thì \(\Delta ABC\backsim\Delta A'B'C'\) theo tỉ số nào?
Phương pháp giải:
Hai tam giác bằng nhau thì các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Tỉ số đồng dạng là tỉ số các cạnh tương ứng.
Lời giải chi tiết:
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).
TH2
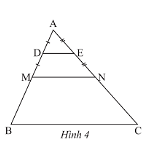
Quan sát Hình 4, cho biết \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,DE\) là đường trung bình của tam giác \(AMN,MN\) là đường trung bình của tam giác \(ABC.\) Tam giác \(ADE\) đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng là bao nhiêu?
Phương pháp giải:
Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu
\(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\end{array} \right.\)
Tỉ số đồng dạng là \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\)
Lời giải chi tiết:
Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)
Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)
Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)
\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)
Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\) nên \(\Delta ADE\backsim\Delta ABC\)
Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).
Vậy tỉ số đồng dạng là \(\frac{1}{4}\).
HĐ4
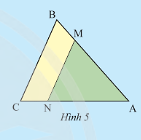
Quan sát Hình 5, biết \(MN//BC\). Hãy điển ? cho thích hợp.
\(\Delta AMN\) và\(\Delta ABC\) có:
\(\widehat A\) chung;
\(\widehat M = ?\);
\(\widehat N = ?\);
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{?}{?}\)
Nêu nhận xét về mối quan hệ giữa tam giác \(AMN\) và tam giác \(ABC\).
Phương pháp giải:
- Tính chất hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì sẽ tạo ra các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.
- Hệ quả định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
Vì \(MN//BC\) nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\) (các cặp góc đồng vị)
Xét tam giác \(ABC\) có, \(MN//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Vậy trong các ô trống cần điền là:
\(\widehat A\) chung;
\(\widehat M = \widehat B\);
\(\widehat N = \widehat C\);
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Tam giác \(\Delta AMN\) và\(\Delta ABC\) có các góc tương ứng bằng nhau và tỉ số các cạnh tương ứng bằng nhau nên \(\Delta AMN\) đồng dạng \(\Delta ABC\).
TH3
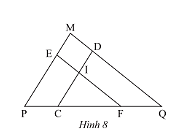
Quan sát Hình 8, cho biết \(DC//MP,EF//MQ\).
a) Chứng minh rằng \(\Delta EPF\backsim\Delta DCQ\).
b) \(\Delta ICF\) có đồng dạng với \(\Delta MPQ\)không? Tại sao?
Phương pháp giải:
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) và \(\Delta ABC\backsim\Delta A''B''C''\) thì \(\Delta A'B'C'\backsim\Delta A''B''C''\).
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết:
a) Xét tam giác \(MPQ\)có \(EF//MQ\) nên \(\Delta MPQ\backsim\Delta EPF\) (định lí) (1)
Xét tam giác \(MPQ\)có \(DC//MP\) nên \(\Delta MPQ\backsim\Delta DCQ\) (định lí) (2)
Từ (1) và (2) \(\Delta EPF\backsim\Delta DCQ\) (tính chất tam giác đồng dạng)
b) Xét tam giác \(EPF\)có \(IC//EP\) nên \(\Delta ICF\backsim\Delta EPF\) (định lí) (3)
Từ (1) và (3) suy ra, \(\Delta ICF\backsim\Delta MPQ\).
VD
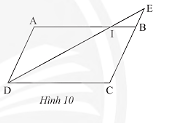
Trong Hình 10, cho biết \(ABCD\) là hình bình hành.
a) Chứng minh rằng \(\Delta IEB\backsim\Delta IDA\).
b) Cho biết \(CB = 3BE\) và \(AI = 9cm\). Tính \(DC\).
Phương pháp giải:
Nếu một đường thẳng cắt phần kéo dài của hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết:
a) Do \(ABCD\) là hình bình hành nên \(BC//AD \Rightarrow EB//AD\)
Xét tam giác \(IDA\) có
\(EB//AD;EB\) cắt \(AI;ID\) tại \(B;E\).
Do đó, \(\Delta IEB\backsim\Delta IDA\) (định lí)
b) Ta có: \(\Delta IEB\backsim\Delta IDA \Rightarrow \frac{{IB}}{{IA}} = \frac{{BE}}{{DA}}\) (hai cặp cạnh tương ứng tỉ lệ).
Mà \(CB = AD;CB = 3BE \Rightarrow AD = 3BE;AI = 9cm\) nên ta có:
\(\frac{{IB}}{9} = \frac{{BE}}{{3BE}} = \frac{1}{3} \Rightarrow IB = \frac{{9.1}}{3} = 3(cm)\).
\(\Rightarrow AB = AI + IB = 9 + 3 = 12cm\) Mà DC = AB (ABCD là hình bình hành \(\Rightarrow DC = 12cm\)
Vậy \(DC = 12cm.\)