Giải mục 3 trang 102 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song (Delta ) và (Delta '). Xét điểm (A) trên đường thẳng (Delta ).
Hoạt động 2
Trong Hình 64 , hai mép của con đường gợi nên hình ảnh hai đường thẳng song song \(\Delta \) và \(\Delta '\). Xét điểm \(A\) trên đường thẳng \(\Delta \).
a) Khoảng cách từ điểm \(A\) đến đường thẳng \(\Delta '\) có phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \) hay không? Vì sao?
b) Khoảng cách đó gợi nên khái niệm gì trong hình học liên quan đến hai đường thẳng song song \(\Delta \) và \(\Delta '\)?
Phương pháp giải:
Sử dụng tính chất của hai đường thẳng song song.
Lời giải chi tiết:
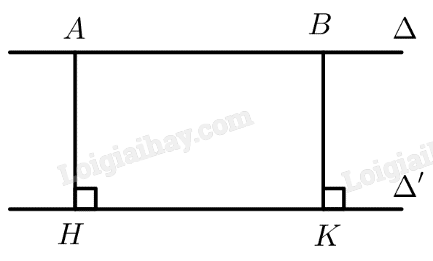
a) Trên đường thẳng \(\Delta \) lấy điểm \(B\) khác \(A\).
Kẻ \(AH \bot \Delta ',BK \bot \Delta '\left( {H,K \in \Delta '} \right)\)
\(ABKH\) là hình chữ nhật \( \Rightarrow AH = BK\)
\( \Rightarrow d\left( {A,\Delta '} \right) = d\left( {B,\Delta '} \right)\)
Vậy khoảng cách từ điểm \(A\) đến đường thẳng \(\Delta '\) không phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \).
b) Khoảng cách đó gợi nên khái niệm khoảng cách giữa hai đường thẳng song song.
Luyện tập 2
Người ta dựng các cột đèn vuông góc với mặt đường, trong đó mỗi cột đèn gợi nên hình ảnh một đường thẳng. Khoảng cách giữa hai chân cột đèn liên tiếp đo được là 5 m. Tại sao có thể nói khoảng cách giữa hai cột đèn đó là 5 m.
Phương pháp giải:
Dựa vào định nghĩa: Khoảng cách giữa hai đường thẳng song song \(\Delta ,\Delta '\) là khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia.
Lời giải chi tiết:
Các cột đèn được dựng thẳng đứng và vuông góc với mặt đường thì chúng song song với nhau. Do đó, đoạn thẳng nối hai chân cột chính là khoảng cách giữa hai đường thẳng song song. Vậy ta có thể nói khoảng cách giữa hai cột đèn đó là 5 m.