Giải mục 4 trang 22 SGK Toán 11 tập 2 - Cánh Diều — Không quảng cáo

LT 7

Cho hai đường thẳng song song \({d_1}\) và \({d_2}\). Trên \({d_1}\) lấy 17 điểm phân biệt, trên \({d_2}\) lấy 20 điểm phân biệt. Chọn Ngẫu nhiên 3 điểm, tính xác suất để các điểm này tạo thành 3 đỉnh của một tam giác.

Phương pháp giải:

Dựa vào các kiến thức vừa học để xác định

Lời giải chi tiết:

Mỗi cách chọn 3 điểm trong 37 điểm là một tổ hợp chập 3 của 37 phần tử. Do đó, không gian mẫu gồm các tổ hợp chập 3 của 27 phần tử và: \(n\left( \Omega  \right) = C_{37}^3 = 7770\)

TH1: 1 điểm nằm trên \({d_1}\) và 2 điểm nằm trên \({d_2}\). Số kết quả thuận lợi cho biến cố này là:

\(n\left( A \right) = C_{17}^1.C_{20}^2 = 3230\)

TH2: 2 điểm nằm trên \({d_1}\) và 1 điểm nằm trên \({d_2}\). Số kết quả thuận lợi cho biến cố này là:

\(n\left( B \right) = C_{17}^2.C_{20}^1 = 2720\)

Vậy xác suất để các điểm lấy ra tạo thành tam giác là: \(P\left( C \right) = \frac{{2720 + 3230}}{{7770}} = \frac{{85}}{{111}}\)

HĐ 7

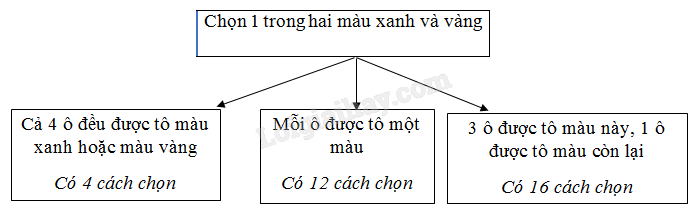
Để trang trí một tờ giấy có dạng hình chữ nhật, bạn Thùy chia tờ giấy đó thành bốn hình chữ nhật nhỏ bằng nhau. Mỗi hình chữ nhật nhỏ được tô bằng một trong hai màu xanh hoặc vàng. Vẽ sơ đồ hình cây biểu thị các khả năng mà bạn Thùy có thể tô màu trang trí cho tờ giấy đó.

Phương pháp giải:

Xác định các trường hợp có thể xảy ra rồi vẽ sơ đồ cây.

Lời giải chi tiết:

LT 8

Một hộp có 5 viên bi màu xanh, 6 viên bi màu đỏ và 7 viên bi màu vàng. Chọn ngẫu nhiên 5 viên bi trong hộp. Tính xác suất để 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng.

Phương pháp giải:

Dựa vào kiến thức vừa học để xác định

Lời giải chi tiết:

\(n\left( \Omega  \right) = C_{18}^5 = 8568\)

TH1: Lấy 1 bi màu xanh, 2 bi màu đỏ và 2 bi màu vàng:\(n\left( A \right) = C_5^1.C_6^2.C_7^2 = 1575\)

TH2: Lấy 3 bi màu xanh, 1 bi màu đỏ và 1 bi màu vàng: \(n\left( B \right) = C_5^3.C_6^1.C_7^1 = 420\)

Xác suất để 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng là:

\(P\left( C \right) = \frac{{1575 + 420}}{{8568}} = \frac{{95}}{{408}}\)