Giải mục 4 trang 10, 11 SGK Toán 11 tập 2 - Chân trời sáng tạo
Ta biết rằng, (sqrt 2 ) là một số vô tỉ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn:
Hoạt động 4
Ta biết rằng, \(\sqrt 2 \) là một số vô tỉ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: \(\sqrt 2 = 1,414213562...\)
Cũng có thể coi \(\sqrt 2 \) là giới hạn của dãy số hữu tỉ \(\left( {{r_n}} \right)\):
\(1,4;1,41;1,414;1,4142;...\)
Từ đây, ta lập dãy số các luỹ thừa \(\left( {{3^{{r_n}}}} \right)\).
a) Bảng dưới cho biết những số hạng đầu tiên của dãy số \(\left( {{3^{{r_n}}}} \right)\) (làm tròn đến chữ số thập phân thứ chín). Sử dụng máy tính cầm tay, hãy tính số hạng thứ 6 và thứ 7 của dãy số này.
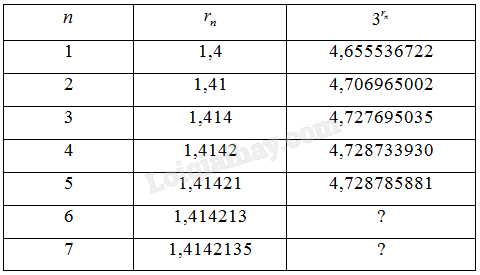
b) Nêu nhận xét về dãy số \(\left( {{3^{{r_n}}}} \right)\).
Phương pháp giải:
Sử dụng máy tính cầm tay để tính.
Lời giải chi tiết:
a) \({r_6} = {3^{1,414213}} = 4,728801466;{r_7} = {3^{1,4142134}} = 4,728803544\).
b) Ta thấy khi \(n \to + \infty \) thì \({3^{{r_n}}} \to {3^{\sqrt 2 }}\).
Thực hành 5
Sử dụng máy tính cầm tay, tính các luỹ thừa sau đây (làm tròn đến chữ số thập phân thứ sáu):
a) \(1,{2^{1,5}}\);
b) \({10^{\sqrt 3 }}\);
c) \({\left( {0,5} \right)^{ - \frac{2}{3}}}\).
Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
Để làm tròn đến chữ số thập phân thứ 6:
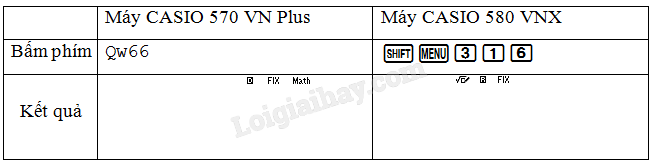
a,

b,

c,
