Giải mục 4 trang 22, 23 SGK Toán 11 tập 1 - Chân trời sáng tạo — Không quảng cáo

Hoạt động 4

Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác $\alpha  = \frac{{\alpha  + \beta }}{2},\beta  = \frac{{\alpha  - \beta }}{2}$ ta được đẳng thức nào?

Phương pháp giải:

Áp dụng công thức:

$\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\end{array}$

Lời giải chi tiết:

Ta có:

$\begin{array}{l}\cos \alpha \cos \beta  = \cos \frac{{\alpha  + \beta }}{2}\cos \frac{{\alpha  - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha  + \beta }}{2} + \frac{{\alpha  - \beta }}{2}} \right) + \cos \left( {\frac{{\alpha  + \beta }}{2} - \frac{{\alpha  - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \alpha  + \cos \beta } \right)\end{array}$

$\begin{array}{l}\sin \alpha \sin \beta  = \sin \frac{{\alpha  + \beta }}{2}\sin \frac{{\alpha  - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha  + \beta }}{2} - \frac{{\alpha  - \beta }}{2}} \right) - \cos \left( {\frac{{\alpha  + \beta }}{2} + \frac{{\alpha  - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \beta  - \cos \alpha } \right)\end{array}$

$\begin{array}{l}\sin \alpha \cos \beta  = \sin \frac{{\alpha  + \beta }}{2}\cos \frac{{\alpha  - \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha  + \beta }}{2} + \frac{{\alpha  - \beta }}{2}} \right) + \sin \left( {\frac{{\alpha  + \beta }}{2} - \frac{{\alpha  - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin \alpha  + \sin \beta } \right)\end{array}$

Thực hành 4

Tính $\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}}$.

Phương pháp giải:

Áp dụng công thức:

$\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}$.

Lời giải chi tiết:

Ta có:

$\begin{array}{l}\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}} = 2\cos \frac{{\frac{{7\pi }}{{12}} + \frac{\pi }{{12}}}}{2}\cos \frac{{\frac{{7\pi }}{{12}} - \frac{\pi }{{12}}}}{2}\\ = 2.\frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 2 }}{2}\end{array}$.

Vận dụng

Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính $\sin \alpha$ và $\cos \alpha$, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.

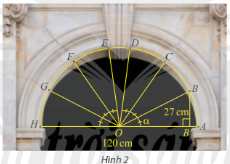
Phương pháp giải:

Quan sát hình vẽ để trả lời.

Lời giải chi tiết:

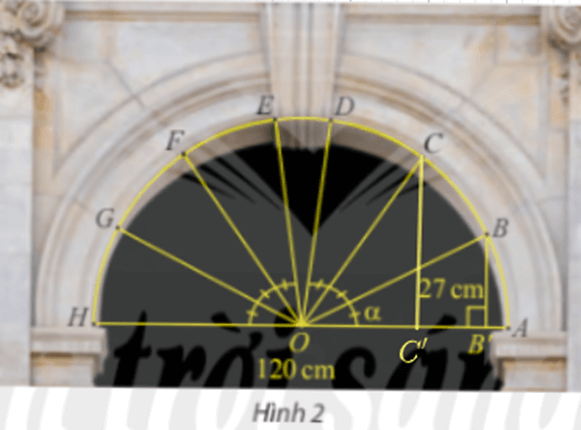
Ta có: $OA = OB = 120:2 = 60$.

Xét tam giác OBB’ có:

$\sin \widehat {BOB'} = \frac{{BB'}}{{OB}} = \frac{{27}}{{60}} = \frac{9}{{20}}$.

Ta có: $\widehat {AOC} = 2\widehat {BOB'}$.

Xét tam giác OCC’ vuông tại C’ có:

$\begin{array}{l}\sin \widehat {COC'} = \frac{{CC'}}{{OC}}\\ \Leftrightarrow CC' = OC.\sin \widehat {COC'} = OC.\sin \left( {2\widehat {BOB'}} \right)\end{array}$.

Mà $\sin \left( {2\widehat {BOB'}} \right) = 2.\sin \widehat {BOB'}.cos\widehat {BOB'}$.

$= 2.\frac{9}{{20}}.\frac{{\sqrt {319} }}{{20}} = \frac{{9\sqrt {319} }}{{400}}$.

Vậy khoảng cách từ C đến AH là $60.\frac{{9\sqrt {319} }}{{200}} \approx 48,2cm$.