Giải mục 4 trang 96, 97, 98 SGK Toán 11 tập 1 - Chân trời sáng tạo
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?
Hoạt động 10
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?

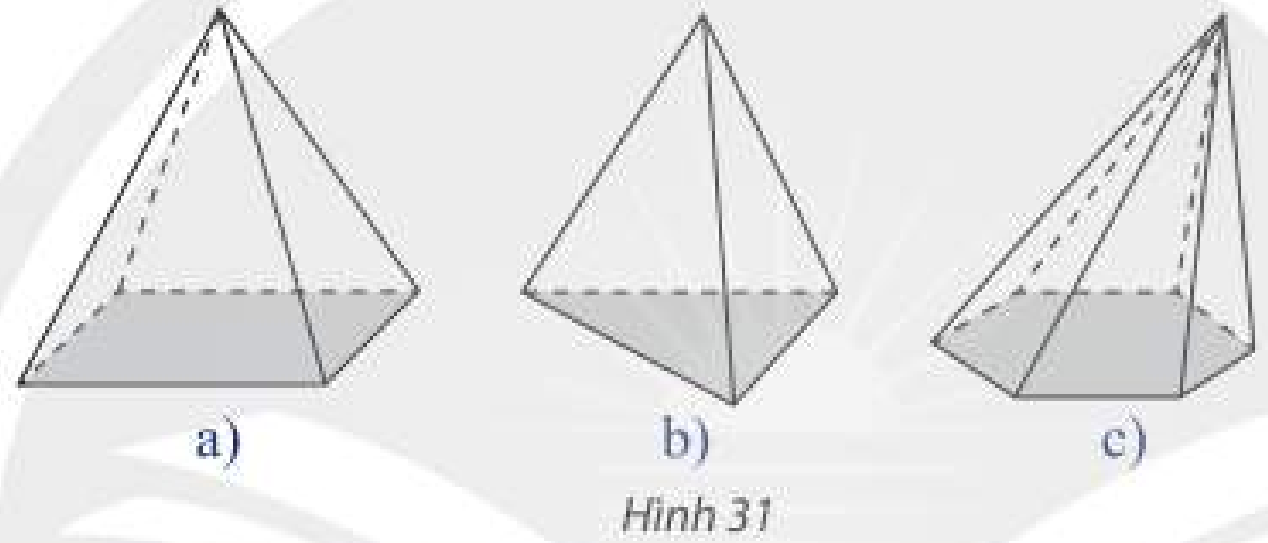
b) Tìm điểm giống nhau của các hình trong Hình 31.
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình tam giác.
b) Điểm giống nhau của các hình trong Hình 31 là: có các mặt bên là hình tam giác.
Hoạt động 11
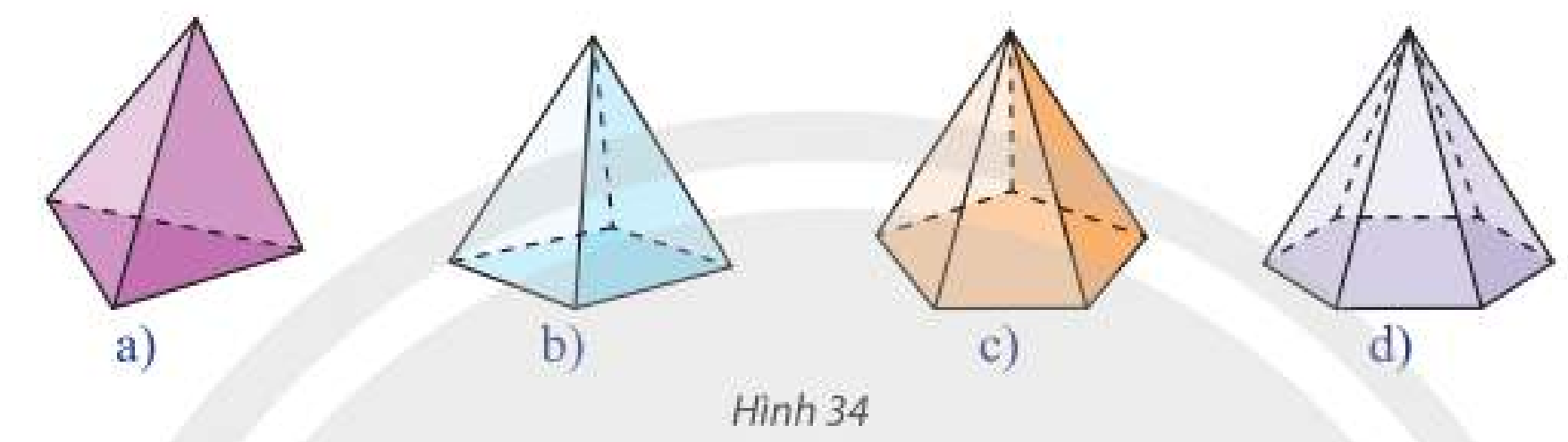
Trong Hình 34, hình chóp nào có số mặt ít nhất?
Phương pháp giải:
Quan sát hình ảnh và đếm số mặt của hình.
Lời giải chi tiết:
Hình chóp a) có 4 mặt.
Hình chóp b) có 5 mặt.
Hình chóp c) có 6 mặt.
Hình chóp d) có 7 mặt.
Vậy hình a) có số mặt ít nhất.
Thực hành 8
Cho tứ diện \(SABC\). Gọi \(H,K\) lần lượt là hai điểm trên hai cạnh \(SA\) và \(SC\left( {H \ne S,A;K \ne S,C} \right)\) sao cho \(HK\) không song song với \(AC\). Gọi \(I\) là trung điểm của \(BC\) (Hình 38).
a) Tìm giao điểm của đường thẳng \(HK\) và mặt phẳng \(\left( {ABC} \right)\).
b) Tìm giao tuyến của các mặt phẳng \(\left( {SAI} \right)\) và \(\left( {ABK} \right)\); \(\left( {SAI} \right)\) và \(\left( {BCH} \right)\).

Phương pháp giải:
‒ Để tìm giao điểm của đường thẳng và mặt phẳng, ta tìm giao điểm của đường thẳng đó với một đường thẳng trong mặt phẳng.
‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt của hai mặt phẳng đó.
Lời giải chi tiết:
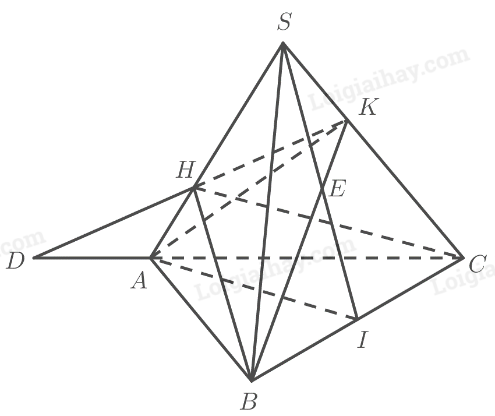
a) Gọi \(D = HK \cap AC\). Ta có:
\(\left. \begin{array}{l}D \in AC \subset \left( {ABC} \right)\\D \in HK\end{array} \right\} \Rightarrow M = HK \cap \left( {ABC} \right)\)
b) Gọi \(E = SI \cap BK\). Ta có:
\(\left. \begin{array}{l}E \in SI \subset \left( {SAI} \right)\\E \in BK \subset \left( {ABK} \right)\end{array} \right\} \Rightarrow E \in \left( {SAI} \right) \cap \left( {ABK} \right)\)
Mà \(A \in \left( {SAI} \right) \cap \left( {ABK} \right)\).
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {ABK} \right)\) là đường thẳng \(AE\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in \left( {SAI} \right)\\I \in BC \subset \left( {BCH} \right)\end{array} \right\} \Rightarrow I \in \left( {SAI} \right) \cap \left( {BCH} \right)\\\left. \begin{array}{l}H \in SA \subset \left( {SAI} \right)\\H \in \left( {BCH} \right)\end{array} \right\} \Rightarrow H \in \left( {SAI} \right) \cap \left( {BCH} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {BCH} \right)\) là đường thẳng \(HI\).
Vận dụng 4
Cho hình chóp \(S.ABCD\). Trên các cạnh bên của hình chóp lấy lần lượt các điểm \(A',B',C',D'\). Cho biết \(AC\) cắt \(B{\rm{D}}\) tại \(O\), \(A'C'\) cắt \(B'{\rm{D'}}\) tại \(O'\), \(AB\) cắt \(DC\) tại \(E\) và \(A'B'\) cắt \(D'C'\) tại \(E'\) (Hình 39). Chứng minh rằng:
a) \(S,O',O\) thẳng hàng;
b) \(S,E',E\) thẳng hàng.
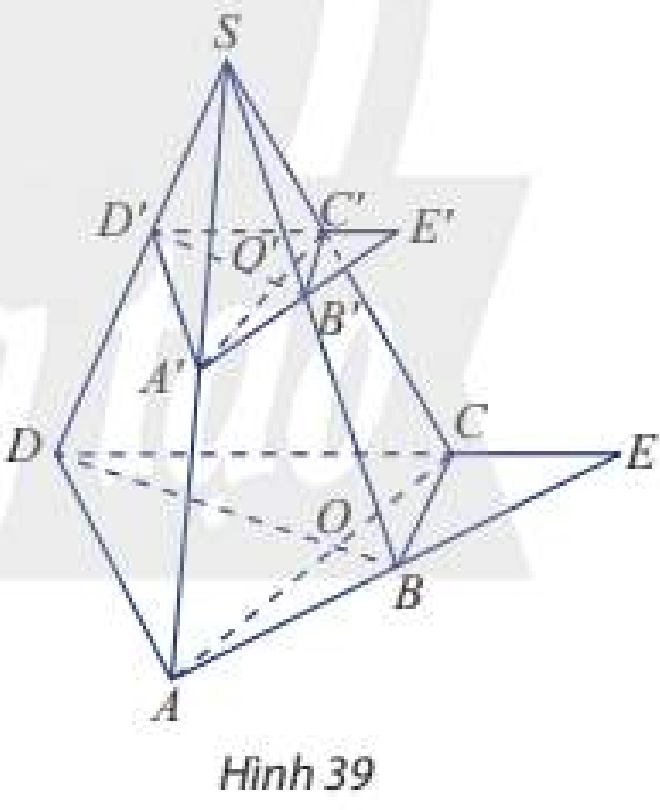
Phương pháp giải:
Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm đó cùng thuộc giao tuyến của hai mặt phẳng.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in BD \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}O' \in A'C' \subset \left( {SAC} \right)\\O' \in B'D' \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O' \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)
Do đó, \(S,O,O'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Vậy \(S,O',O\) thẳng hàng.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in AB \subset \left( {SAB} \right)\\E \in CD \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\\\left. \begin{array}{l}E' \in A'B' \subset \left( {SAB} \right)\\E' \in C'D' \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E' \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\)
Do đó, \(S,E,E'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\).
Vậy \(S,E,E'\) thẳng hàng.
Vận dụng 5
Nêu cách tạo lập tứ diện đều \(SABC\) từ tam giác đều \(SS'S''\) theo gợi ý ở Hình 40.
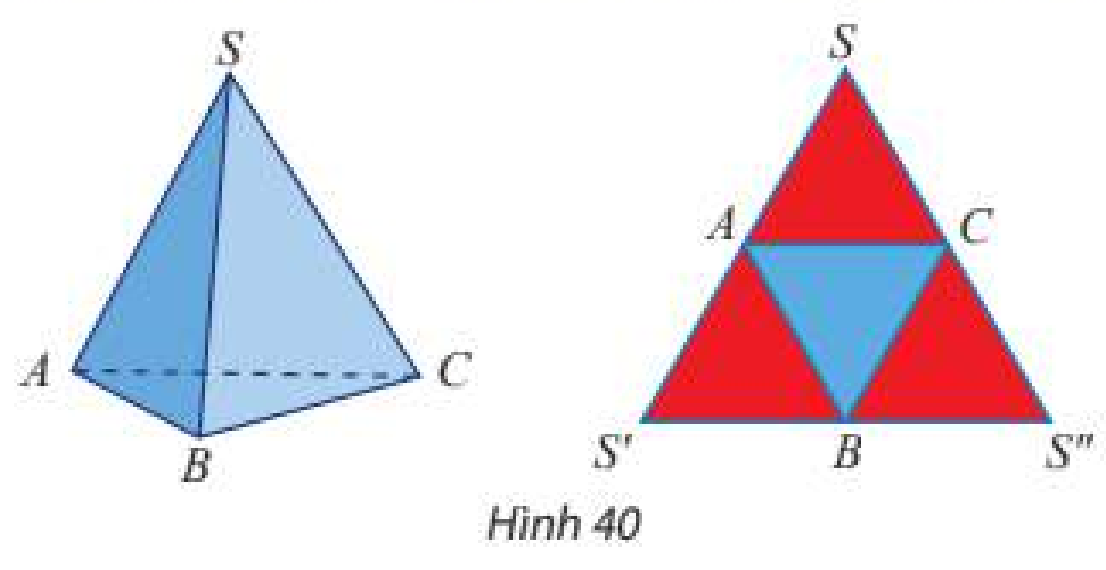
Phương pháp giải:
Để dựng được tứ diện đều, ta dựng một hình tứ diện có bốn mặt là các tam giác đều.
Lời giải chi tiết:
• Cách dựng:
Bước 1: Gọi \(A,B,C\) lần lượt là trung điểm của \(SS',S'S'',SS''\).
Bước 2: Gấp các đường \(AB,BC,AC\) sao cho các điểm \(S,S',S''\) trùng nhau.
Khi đó, ta được tứ diện đều \(SABC\).
• Chứng minh:
Vì \(A,B,C\) lần lượt là trung điểm của \(SS',S'S'',SS''\) nên theo tính chất đường trung bình của tam giác, ta có: \(SA = S'A = S'B = S''B = SC = S'C = AB = BC = AC = \frac{1}{2}SS'\).
Do vậy các tam giác \(SAC,S'AB,S''BC,ABC\) là các tam giác đều.
Vậy tứ diện \(SABC\) có các mặt \(SAC,SAB,SBC,ABC\) là các tam giác đều nên tứ diện \(SABC\) là tứ diện đều.