Giải mục 5 trang 38, 39 SGK Toán 11 tập 1 - Chân trời sáng tạo — Không quảng cáo

Hoạt động 5

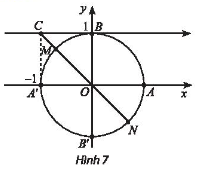
Trong mặt phẳng toạ độ Oxy, cho C là điểm trên trục côtang có toạ độ là (-1; 1) (Hình 7). Những điểm nào biểu diễn góc lượng giác x có $cotx =  - 1$? Xác định số đo của các góc lượng giác đó.

Phương pháp giải:

Quan sát hình vẽ để trả lời.

Lời giải chi tiết:

Trên đường tròn lượng giác hai điểm M và N biểu diễn các góc lượng giác có số đo góc x thỏa mãn $cotx =  - 1$.

Điểm M biểu diễn các góc lượng giác có số đo góc $\frac{{3\pi }}{4} + k2\pi ,k \in \mathbb{Z}$.

Điểm N biểu diễn các góc lượng giác có số đo góc $- \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}$.

Thực hành 5

Giải các phương trình sau:

$\begin{array}{*{20}{l}}{a){\rm{ }}cotx = 1;}\\{b){\rm{ }}cot\left( {3x + 30^\circ } \right) = cot75^\circ .}\end{array}$

Phương pháp giải:

Với mọi $m \in \mathbb{R}$, tồn tại duy nhất $\alpha  \in \left( {0;\pi } \right)$ thoả mãn $\cot \alpha  = m$. Khi đó:

$\cot {\rm{x}} = m \Leftrightarrow \cot x = \cot \alpha  \Leftrightarrow x = \alpha  + k\pi ,k \in \mathbb{Z}.$

$\cot x = \cot {\alpha ^o} \Leftrightarrow x = {\alpha ^o} + k{180^o},k \in \mathbb{Z}.$

Lời giải chi tiết:

a) Vì $cotx = 1$nên phương trình $cotx = 1$ có các nghiệm là $x = \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}$.

Vậy tập nghiệm của phương trình là: $S = \left\{ {\frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}$.

$\begin{array}{*{20}{l}}{b){\rm{ }}cot\left( {3x + 30^\circ } \right) = cot75^\circ }\\{ \Leftrightarrow \;3x + 30^\circ  = 75^\circ  + k180^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}}\\{ \Leftrightarrow \;3x = 45^\circ  + k180^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}.}\\{ \Leftrightarrow \;x = 15^\circ  + k60^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}}\end{array}$

Vậy tập nghiệm của phương trình là: $S = \{ 15^\circ  + k60^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}\} .$