Giải mục 7 trang 47 Chuyên đề học tập Toán 10 - Cánh diều — Không quảng cáo

HĐ 9

Vẽ elip (E): $\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1$

Lời giải chi tiết:

Để vẽ elip (E), ta có thể làm như sau:

Ta thấy $a = 5,b = 3$. (E) có các đỉnh ${A_1}\left( { - 5;0} \right),{A_2}\left( {5;0} \right),{B_1}\left( {0; - 3} \right),{B_2}\left( {0;3} \right)$

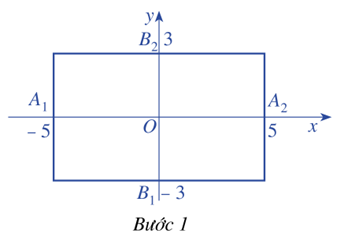
Bước 1: Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn thường thẳng $x =  - 5,x = 5,y =  - 3,y = 3$

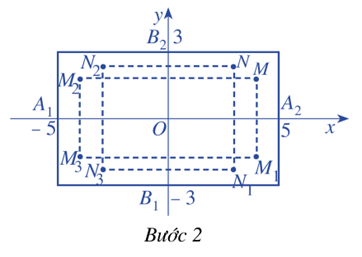
Bước 2: Tìm một số điểm cụ thể thuộc elip, chẳng hạn, ta thấy điểm $M\left( {4;\frac{9}{5}} \right)$ và điểm $N\left( {3;\frac{{12}}{5}} \right)$ thuộc (E) và điểm ${M_1}\left( {4; - \frac{9}{5}} \right),{M_2}\left( { - 4;\frac{9}{5}} \right),{M_3}\left( { - 4; - \frac{9}{5}} \right),{N_1}\left( {3; - \frac{{12}}{5}} \right),{N_2}\left( { - 3;\frac{{12}}{5}} \right),{N_3}\left( { - 3; - \frac{{12}}{5}} \right)$ thuộc (E)

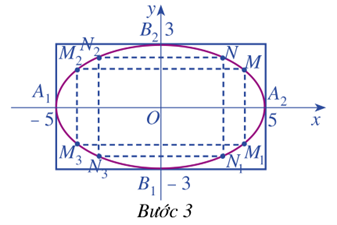
Bước 3: Vẽ đường elip (E) đi qua các điểm cụ thể trên, nằm ở phía trong hình chữ nhật cơ sở và tiếp xúc với các cạnh của hình chữ nhật cơ sở tại bốn điểm của đỉnh (E) là ${A_1}\left( { - 5;0} \right),{A_2}\left( {5;0} \right),{B_1}\left( {0; - 3} \right),{B_2}\left( {0;3} \right)$