Giải mục 4 trang 53 Chuyên đề học tập Toán 10 - Cánh diều — Không quảng cáo

HĐ 5

Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho $\left| {M{F_1} - M{F_2}} \right| = 2a$, ở đó ${F_1}{F_2} = 2c$ với $c > a > 0$. Ta chọn hệ trục tọa độ $Oxy$ có gốc là trung điểm của đoạn thẳng ${F_1}{F_2}$. Trục $Oy$ là đường trung trực của ${F_1}{F_2}$ và ${F_2}$ nằm trên tia $Ox$ (Hình 16).  Khi đó ${F_1}( - c;0),{F_2}(c;0)$ là các tiêu diểm của hypebol (H)

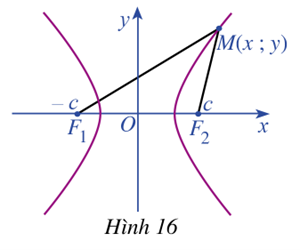
Giả sử điểm $M\left( {x;y} \right)$ thuộc hypebol (H), chứng minh:

a) $M{F_1}^2 = {x^2} + 2cx + {c^2} + {y^2}$

b) $M{F_2}^2 = {x^2} - 2cx + {c^2} + {y^2}$

c) $M{F_1}^2 - M{F_2}^2 = 4cx$

Lời giải chi tiết:

a) Ta có: $\overrightarrow {M{F_1}}  = \left( { - c - x; - y} \right) \Rightarrow M{F_1}^2 = {\left( { - c - x} \right)^2} + {y^2} = {x^2} + 2cx + {c^2} + {y^2}$

b) Ta có: $\overrightarrow {M{F_2}}  = \left( {c - x; - y} \right) \Rightarrow M{F_2}^2 = {\left( {c - x} \right)^2} + {y^2} = {x^2} - 2cx + {c^2} + {y^2}$

c) $M{F_1}^2 - M{F_2}^2 = \left( {{x^2} + 2cx + {c^2} + {y^2}} \right) - \left( {{x^2} - 2cx + {c^2} + {y^2}} \right) = 4cx$

HĐ 6

Với mỗi điểm M thuộc hypebol (H), từ hai đẳng thức $M{F_1}^2 - M{F_2}^2 = 4cx$ và $\left| {M{F_1} - M{F_2}} \right| = 2a$, chứng minh $M{F_1} = \left| {a + \frac{c}{a}x} \right| = \left| {a + ex} \right|$ và $M{F_2} = \left| {a - \frac{c}{a}x} \right| = \left| {a - ex} \right|$

Lời giải chi tiết:

+ Ta có: $M{F_1}^2 - M{F_2}^2 = \left( {M{F_1} - M{F_2}} \right)\left( {M{F_1} + M{F_2}} \right) = \left( {M{F_1} - M{F_2}} \right).\left| {2a} \right| = 4cx$

$\Rightarrow M{F_1} - M{F_2} = \frac{{2c}}{{\left| a \right|}}x$

+ Ta có: $\left\{ \begin{array}{l}M{F_1} + M{F_2} = \left| {2a} \right|\quad \left( 1 \right)\\M{F_1} - M{F_2} = \frac{{2c}}{{\left| a \right|}}x\quad \left( 2 \right)\end{array} \right.$

Từ (1) và (2) suy ra:

$2M{F_1} = \left| {2a} \right| + \frac{{2c}}{{\left| a \right|}}x \Rightarrow M{F_1} = \left| a \right| + \frac{c}{{\left| a \right|}}x = \left| {a + \frac{c}{a}x} \right| = \left| {a + ex} \right|$

$M{F_2} = 2\left| a \right| - M{F_1} = 2\left| a \right| - \left( {\left| a \right| + \frac{c}{{\left| a \right|}}x} \right) = \left| a \right| - \frac{c}{{\left| a \right|}}x$$= \left| {a - \frac{c}{a}x} \right| = \left| {a - ex} \right|$

Luyện tập - vận dụng 3

Cho hypebol (H) có phương trình chính tắc: $\frac{{{x^2}}}{{144}} - \frac{{{y^2}}}{{25}} = 1$. Giả sử điểm M là diderm chuẩn thuộc hypebol có hoành độ là 15. Tìm độ dài các bán kính qua tiêu của điểm M.

Phương pháp giải:

Phương trình của hypebol $\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1$ trong đó $a > 0,b > 0$. Khi đó ta có:

+ Độ dài hai bán kính qua tiêu của điểm $M(x;y)$ là: $M{F_1} = \left| {a + \frac{c}{a}x} \right|;M{F_2} = \left| {a - \frac{c}{a}x} \right|$

Lời giải chi tiết:

Ta có $a = 12,b = 3,c = \sqrt {{a^2} + {b^2}}  = \sqrt {144 + 9}  = 3\sqrt {17}$.

Do đó $e = \frac{{3\sqrt {17} }}{{12}} = \frac{{\sqrt {17} }}{4}$.

Vậy độ dài các bán kính qua tiêu của điểm M là:

$M{F_1} = \left| {12 + \frac{{\sqrt {17} }}{4}.15} \right|;M{F_2} = \left| {12 - \frac{{\sqrt {17} }}{4}.15} \right|$