Hàm số đồng biến - Hàm số nghịch biến - Sự biến thiên của hàm số — Không quảng cáo

1. Lý thuyết

Cho hàm số \(y = f(x)\) xác định trên khoảng (a;b).

+ Định nghĩa:

Hàm số \(y = f(x)\) đồng biến ( tăng ) trên khoảng (a;b) nếu

\(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)

Hàm số \(y = f(x)\) nghịch biến ( giảm ) trên khoảng (a;b) nếu

\(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)

Xét sự biến thiên của hàm số là tìm các khoảng hàm số đồng biến và các khoảng hàm số nghịch biến.

+ Mô tả sự biến thiên bằng bảng biến thiên

Kết quả xét sự biến thiên được tổng kết trong một bảng biến thiên . Trong đó:

Dấu mũi tên đi lên diễn tả hàm số đồng biến trên khoảng tương ứng.

Dấu mũi tên đi xuống diễn tả hàm số nghịch biến trên khoảng tương ứng.

+ Mô tả sự biến thiên bằng đồ thị

Hàm số đồng biến trên khoảng (a;b) khi và chỉ khi đồ thị hàm số  có dạng “ đi lên ” (từ trái sang phải) trên khoảng đó.

Hàm số nghịch biến trên khoảng (a;b) khi và chỉ khi đồ thị hàm số có dạng “ đi xuống ” (từ trái sang phải) trên khoảng đó.

+ Hàm số bậc nhất \(y = ax + b\) đồng biến trên \(\mathbb{R}\) nếu \(a > 0\), nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\).

2. Ví dụ minh họa

Ví dụ 1. Chứng minh hàm số \(y = 2{x^2}\)đồng biến trên khoảng \((0; + \infty )\)

Xét hai số bất kì \({x_1},{x_2} \in (0; + \infty )\) sao cho \({x_1} < {x_2}\).

Ta có: \(0 < {x_1} < {x_2}\) nên \(2{x_1}^2 < 2{x_2}^2\) hay \(f({x_1}) < f({x_2})\)

Vậy hàm số đồng biến trên khoảng \((0; + \infty )\)

Ví dụ 2. Cho bảng biến thiên của hàm số \(y = 2{x^2} + 1\)

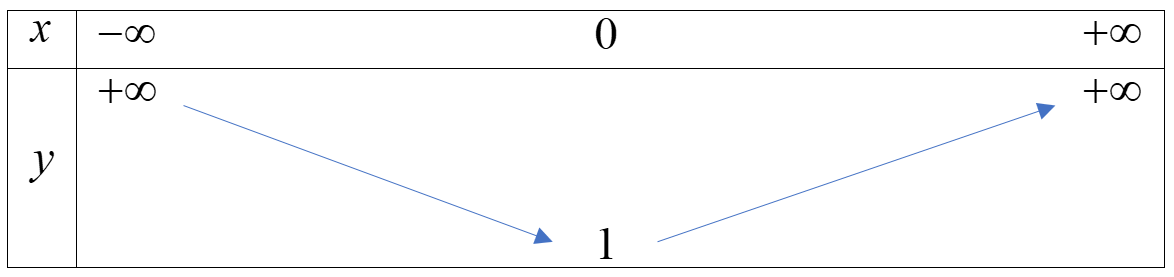
• Dấu mũi tên đi xuống diễn tả hàm số nghịch biến trên khoảng \(( - \infty ;0)\)
• Dấu mũi tên đi lên diễn tả hàm số đồng biến trên khoảng \((0; + \infty )\)

Ví dụ 3. Cho đồ thị của hàm số \(y = f(x)\)

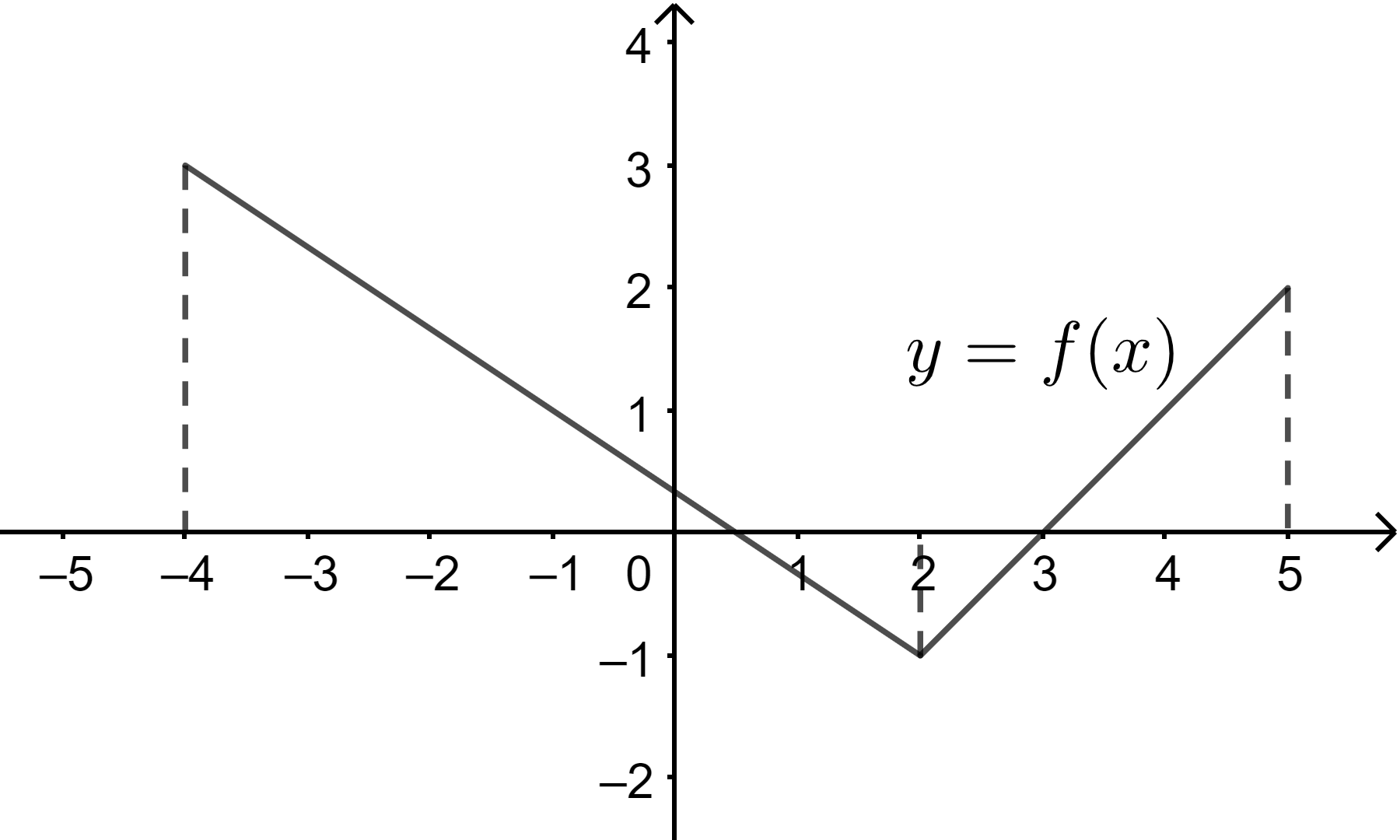
Hàm số \(y = f(x)\) đồng biến trên khoảng (2;5)

Hàm số \(y = f(x)\) nghịch biến trên khoảng (-4;2)