Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Cánh Diều
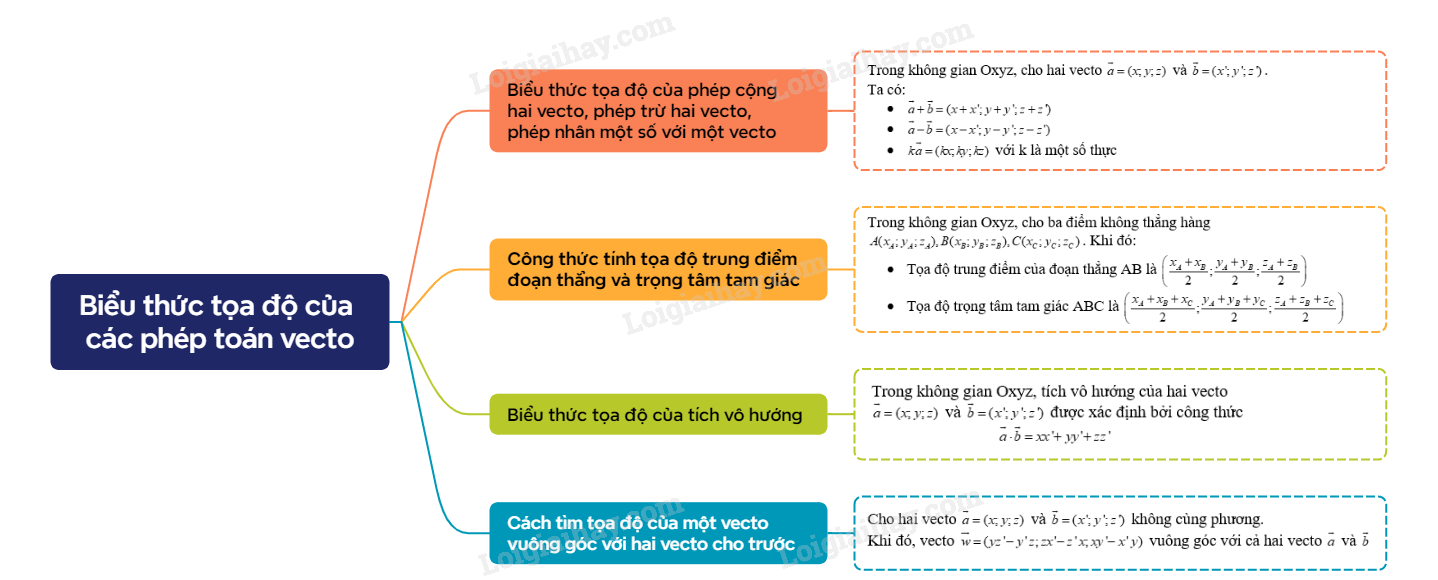
1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
|
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (x;y;z)\) . và \(\overrightarrow b = (x';y';z')\) . Ta có: · \(\overrightarrow a + \overrightarrow b = (x + x';y + y';z + z')\) · \(\overrightarrow a - \overrightarrow b = (x - x';y - y';z - z')\) \(k\overrightarrow a = (kx;ky;kz)\) với k là một số thực |
2. Tọa độ trung điểm đoạn thẳng. Tọa độ trọng tâm tam giác
|
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\) . Khi đó: · Tọa độ trung điểm của đoạn thẳng AB là \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\) Tọa độ trọng tâm tam giác ABC là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{2};\frac{{{y_A} + {y_B} + {y_C}}}{2};\frac{{{z_A} + {z_B} + {z_C}}}{2}} \right)\) |
3. Biểu thức tọa độ của tích vô hướng
| Trong không gian Oxyz, tích vô hướng của hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\) được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = xx' + yy' + zz'\) |
4. Cách tìm tọa độ của một vecto vuông góc với hai vecto cho trước
|
Cho hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\) không cùng phương. Khi đó, vecto \(\overrightarrow w = (yz' - y'z;zx' - z'x;xy' - x'y)\) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) |