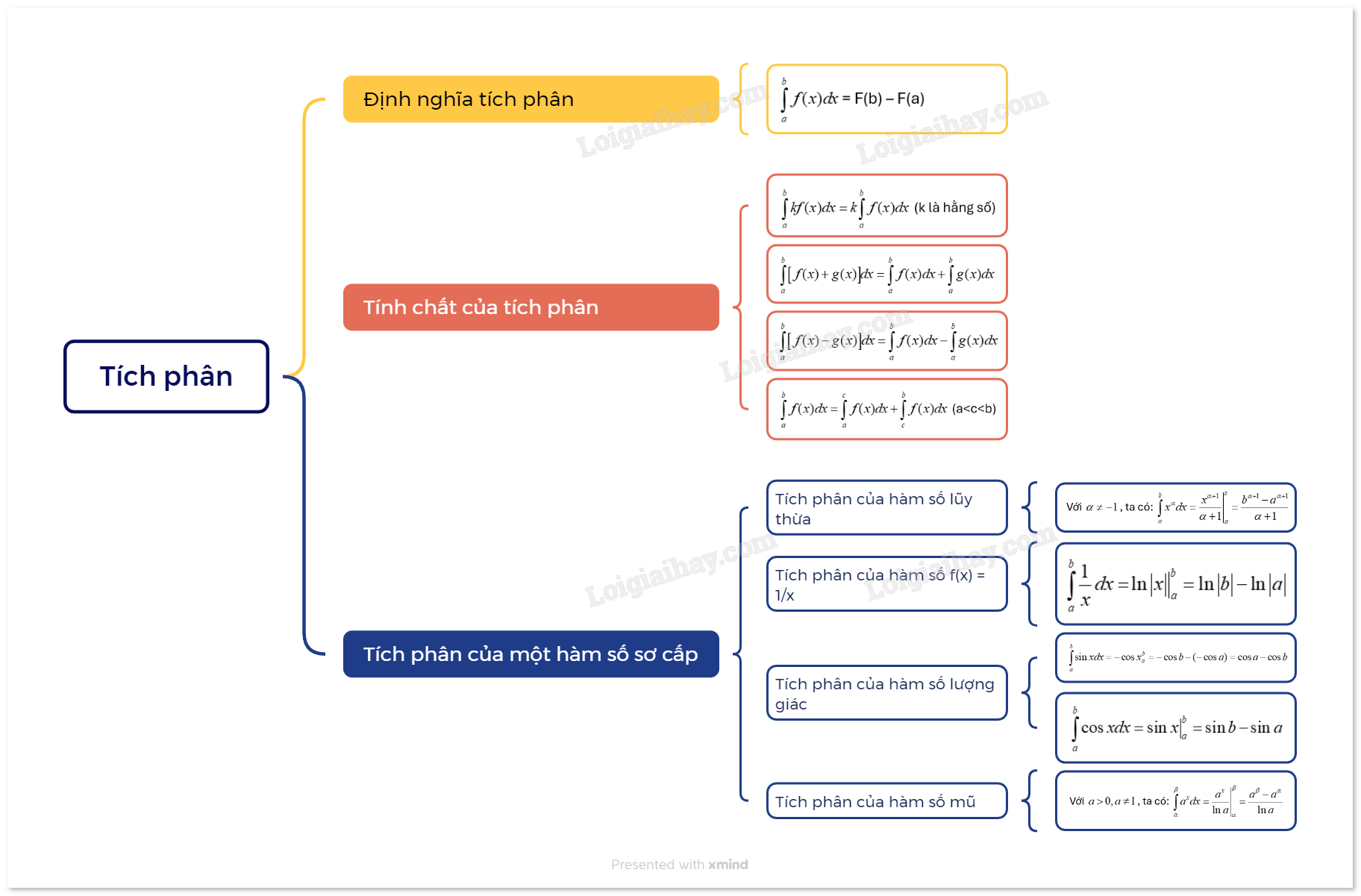
Lý thuyết Lý thuyết Tích phân Toán 12 Cánh Diều
Cho hàm số f(x) liên tục trên đoạn (left[ {a;b} right]). Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn (left[ {a;b} right]) thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là (intlimits_a^b {f(x)dx} ).
1.Định nghĩa tích phân
| Cho hàm số f(x) liên tục trên đoạn \(\left[ {a;b} \right]\). Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\) thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là \(\int\limits_a^b {f(x)dx} \). |
2. Tính chất của tích phân
|
3. Tích phân của một số hàm số sơ cấp
| Với \(\alpha \ne - 1\), ta có: \(\int\limits_a^b {{x^\alpha }dx} = \left. {\frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}} \right|_a^b = \frac{{{b^{\alpha + 1}} - {a^{\alpha + 1}}}}{{\alpha + 1}}\) |
b) Tích phân của hàm số \(f(x) = \frac{1}{x}\)
|
Với hàm số \(f(x) = \frac{1}{x}\) liên tục trên đoạn \(\left[ {a;b} \right]\), ta có: \[\int\limits_a^b {\frac{1}{x}dx = } \left. {\ln \left| x \right|} \right|_a^b = \ln \left| b \right| - \ln \left| a \right|\] |
c) Tích phân của hàm số lượng giác
|
d) Tích phân của hàm số mũ
| Với \(a > 0,a \ne 1\), ta có: \(\int\limits_\alpha ^\beta {{a^x}dx} = \left. {\frac{{{a^x}}}{{\ln a}}} \right|_\alpha ^\beta = \frac{{{a^\beta } - {a^\alpha }}}{{\ln a}}\) |
Cùng chủ đề:
Lý thuyết Lý thuyết Tích phân Toán 12 Cánh Diều