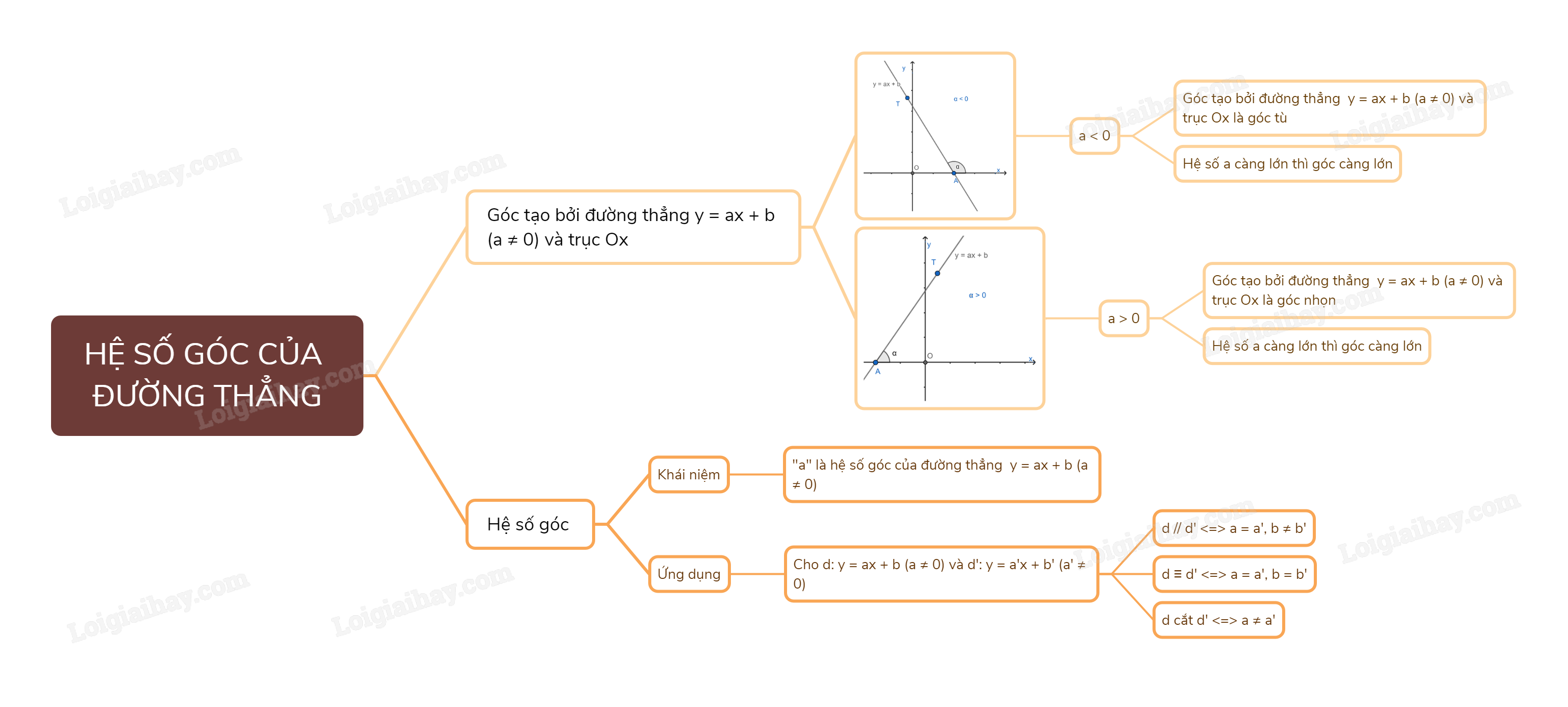
Lý thuyết Hệ số góc của đường thẳng SGK Toán 8 - Kết nối tri thức
Hệ số góc của đường thẳng là gì?
1. Hệ số góc của đường thẳng
Góc tạo bởi đường thẳng y = ax + b (a \( \ne \) 0) và trục Ox.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a\( \ne \)0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.
Góc \(\alpha \) tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc \(\alpha \))
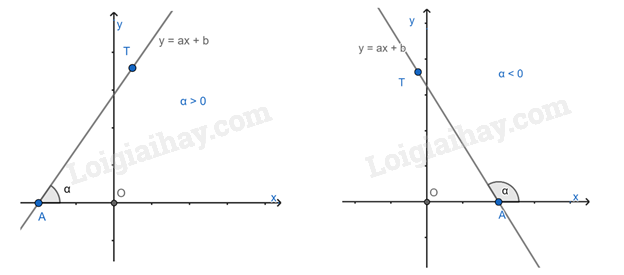
Hệ số góc: Ta gọi a là hệ số góc của đường thẳng y = ax + b (a\( \ne \)0).
Ví dụ: Đường thẳng y = 3x – 1 có hệ số góc là 3;
y = 2 – x có hệ số góc là -1.
2. Nhận biết hai đường thẳng song song
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) song song với nhau khi a = a’; b \( \ne \) b’ và ngược lại.
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) trùng nhau khi a = a’; b = b’ và ngược lại.
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) cắt nhau khi a \( \ne \) a’ và ngược lại.
Ví dụ: Đường thẳng y = -x + 1 và đường thẳng y = -x song song với nhau.
Đường thẳng y = -x + 1 và đường thẳng y = 2x + 1 cắt nhau.