Lý thuyết Hình trụ Toán 9 Cánh diều
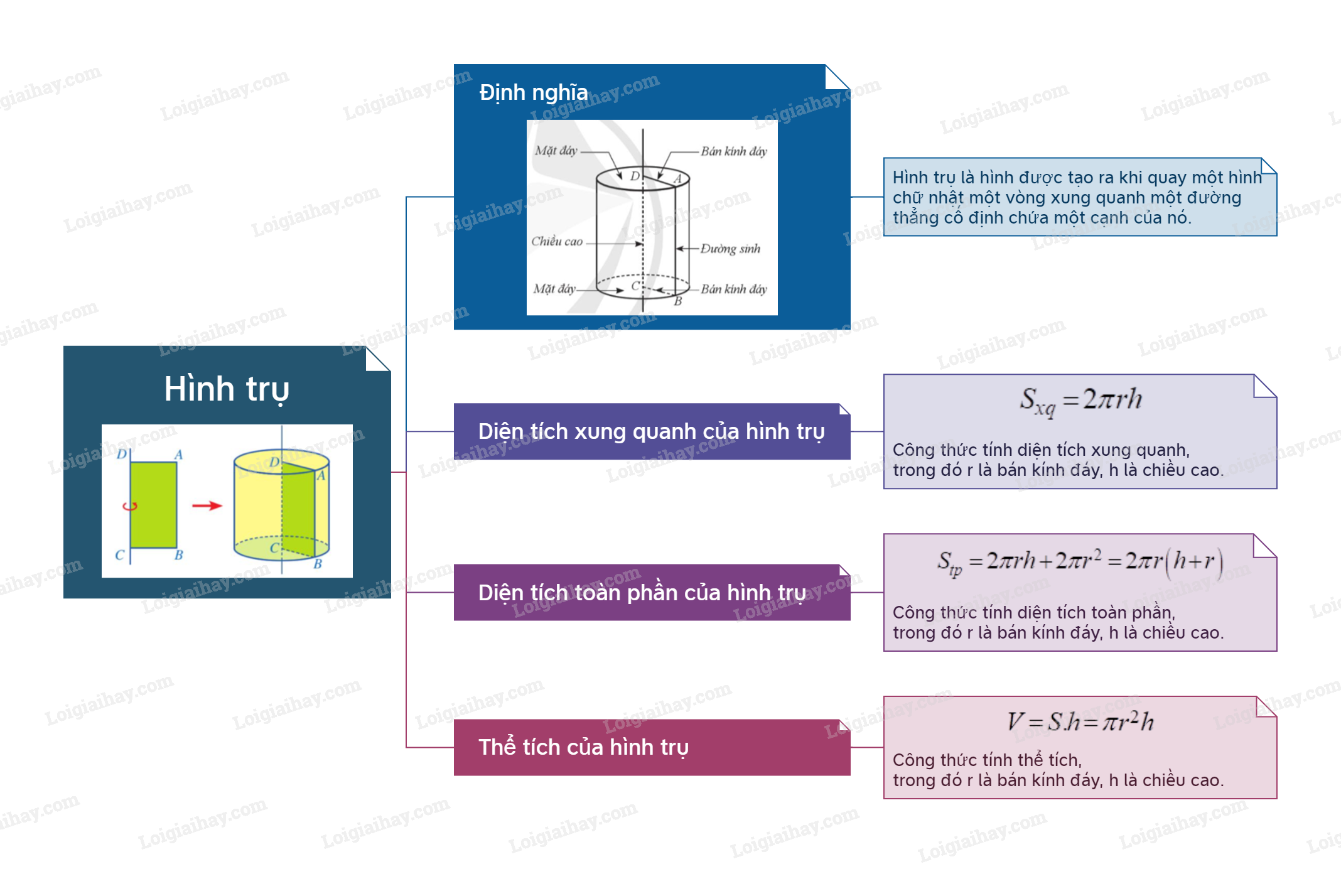
1. Hình trụ Định nghĩa Hình trụ là hình được tạo ra khi quay một hình chữ nhật một vòng xung quanh một đường thẳng cố định chứa một cạnh của nó.
1. Hình trụ
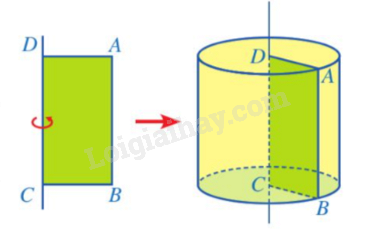
Định nghĩa
|
Hình trụ là hình được tạo ra khi quay một hình chữ nhật một vòng xung quanh một đường thẳng cố định chứa một cạnh của nó. |
Ví dụ:
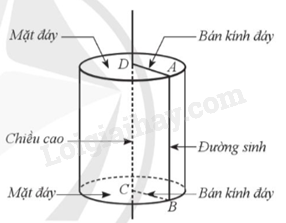
Hình trụ trên có:
- Hình tròn tâm D bán kính DA và hình tròn tâm C bán kính CB là hai mặt đáy;
hai mặt đáy của hình trụ bằng nhau và nằm trong hai mặt phẳng song song;
- Độ dài cạnh DA được gọi là bán kính đáy;
- Độ dài cạnh CD được gọi là chiều cao;
- Cạnh AB quét nên mặt xung quanh của hình trụ, mỗi vị trí của cạnh AB được gọi là một đường sinh; độ dài đường sinh bằng chiều cao của hình trụ.
2. Diện tích xung quanh của hình trụ
Diện tích xung quanh của hình trụ
|
Diện tích xung quanh \({S_{xq}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{xq}} = 2\pi rh\). |
Diện tích toàn phần của hình trụ
|
Diện tích toàn phần \({S_{tp}}\) bằng tổng của diện tích xung quanh và diện tích hai đáy của hình trụ: \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {h + r} \right)\) |
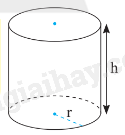
Ví dụ:
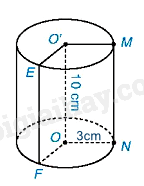
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .3.10 = 60\pi \left( {c{m^2}} \right)\)
3. Thể tích của hình trụ
|
Thể tích V của hình trụ có bán kính đáy r và chiều cao h là: \(V = S.h = \pi {r^2}h\) (S là diện tích đáy của hình trụ).
|
Ví dụ:
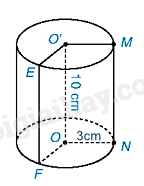
Diện tích đáy là:
\(S = \pi {r^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
Thể tích của hình trụ là:
\(V = S.h = 9\pi .10 = 90\pi \left( {c{m^3}} \right)\)