Lý thuyết Phép quay Toán 9 Cánh diều
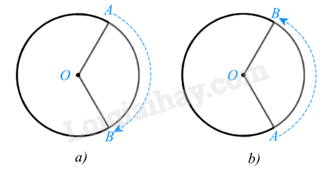
1. Khái niệm - Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \(\alpha ^\circ \) (hình a).
1. Khái niệm
|
- Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \(\alpha ^\circ \) (hình a). Định nghĩa tương tự cho phép quay ngược chiều \(\alpha ^\circ \) tâm O (hình b). Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
|
Phép quay giữ nguyên hình đa giác đều
|
- Cho hình đa giác đều \({A_1}{A_2} \ldots {A_n}(n \ge 3,n \in {\rm{N}})\) có tâm \(O\). Phép quay giữ nguyên hình đa giác đều \({A_1}{A_2} \ldots {A_n}\) là phép quay tâm \(O\) biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đểu đó. - Người ta chứng minh được rằng chỉ có các phép quay sau đây giữ nguyên hình đa giác đều \({A_1}{A_2} \ldots {A_n}(n \ge 3,n \in {\rm{N}})\) với tâm \(O\): các phép quay thuận chiểu \(\alpha ^\circ \) tâm \(O\) và các phép quay ngược chiểu \(\alpha ^\circ \) tâm \(O\), với \(\alpha ^\circ \) lần lượt nhận các giá trị \(\alpha _1^{\rm{o}} = \frac{{360^\circ }}{n};\alpha _2^{\rm{o}} = \frac{{2 \cdot 360^\circ }}{n}; \ldots ;\alpha _n^{\rm{o}} = \frac{{n \cdot 360^\circ }}{n} = 360^\circ \) |
Ví dụ:
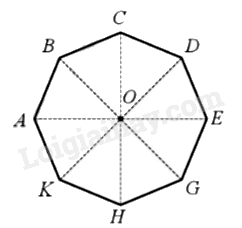
Phép quay thuận chiều \(45^\circ \) tâm O biến điểm A thành điểm B thì phép quay đó biến các điểm C, D, H, K tương ứng thành các điểm D, E, K, A.