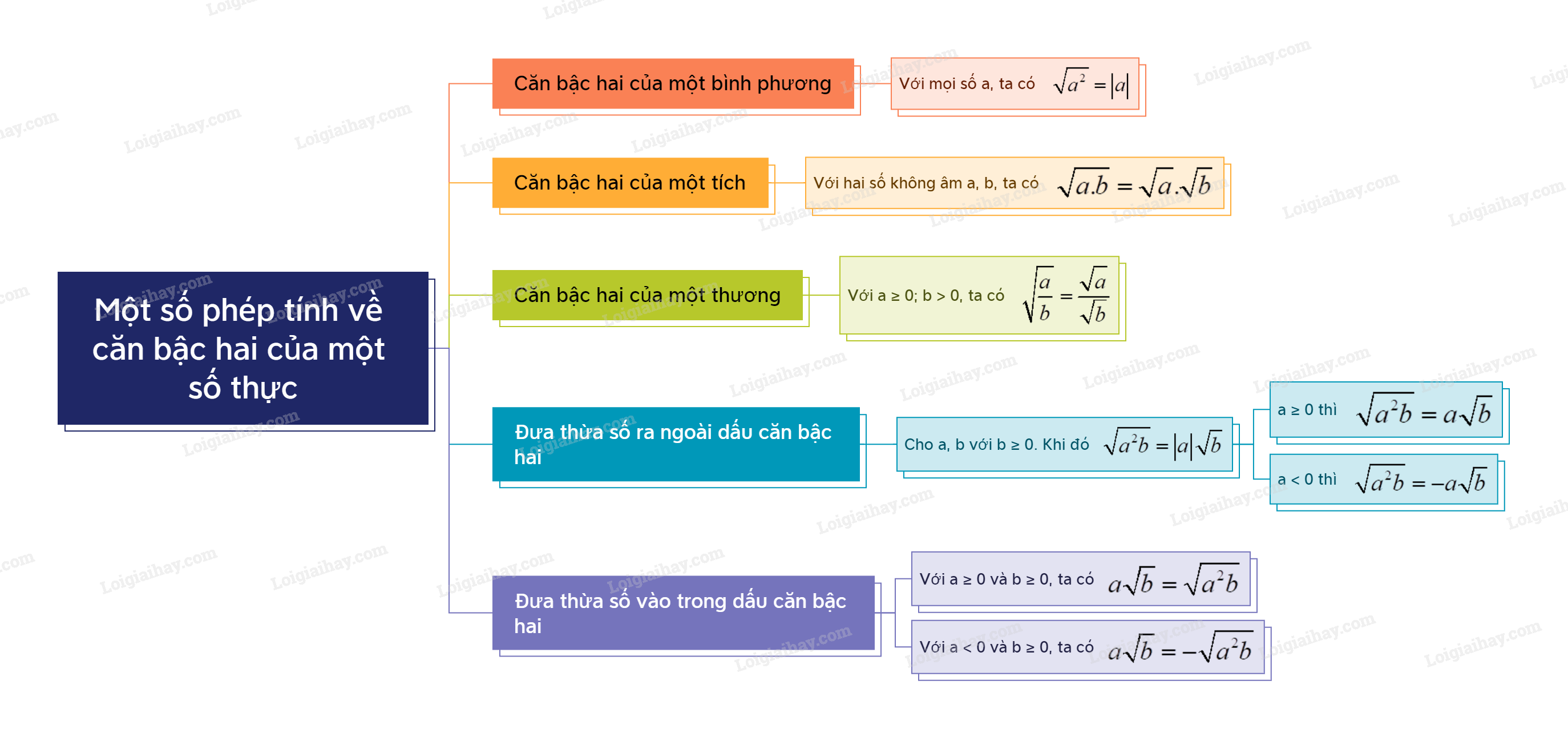
Lý thuyết Một số phép tính về căn bậc hai của một số thực Toán 9 Cánh diều
1. Căn bậc hai của một bình phương Với mọi số a, ta có: \(\sqrt {{a^2}} = \left| a \right|\).
1. Căn bậc hai của một bình phương
|
Với mọi số a, ta có: \(\sqrt {{a^2}} = \left| a \right|\). |
Ví dụ:
\(\sqrt {{{13}^2}} = \left| {13} \right| = 13\); \(\sqrt {{{\left( { - 8} \right)}^2}} = \left| { - 8} \right| = 8\).
2. Căn bậc hai của một tích
|
Với hai số không âm a, b, ta có: \(\sqrt {a.b} = \sqrt a .\sqrt b \). |
Chú ý: Quy tắc trên có thể mở rộng cho tích có nhiều thừa số không âm.
Ví dụ:
\(\sqrt {81.49} = \sqrt {81} .\sqrt {49} = 9.7 = 63\);
\(\sqrt {1,3} .\sqrt {10} .\sqrt {13} = \sqrt {1,3.10.13} = \sqrt {13.13} = \sqrt {{{13}^2}} = 13\).
3. Căn bậc hai của một thương
|
Với \(a \ge 0;b > 0\), ta có: \(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\). |
Ví dụ:
\(\sqrt {\frac{4}{{25}}} = \frac{{\sqrt 4 }}{{\sqrt {25} }} = \frac{2}{5}\);
\(\frac{{\sqrt {216} }}{{\sqrt 6 }} = \sqrt {\frac{{216}}{6}} = \sqrt {36} = 6\). 4. Đưa thừa số ra ngoài dấu căn bậc hai
Phép đưa thừa số ra ngoài dấu căn bậc hai
|
Cho hai số a, b với \(b \ge 0\). Khi đó \(\sqrt {{a^2}b} = \left| a \right|\sqrt b \). Cụ thể, ta có: - Nếu \(a \ge 0\) thì \(\sqrt {{a^2}b} = a\sqrt b \). - Nếu \(a < 0\) thì \(\sqrt {{a^2}b} = - a\sqrt b \). |
Ví dụ:
\(\sqrt {{7^2}.2} = 7\sqrt 2 \);
\(\sqrt {{{\left( { - 11} \right)}^2}.3} = \left| { - 11} \right|.\sqrt 3 = 11\sqrt 3 \).
5. Đưa thừa số vào trong dấu căn bậc hai
Phép đưa thừa số vào trong dấu căn bậc hai
|
- Với \(a \ge 0\) và \(b \ge 0\), ta có: \(a\sqrt b = \sqrt {{a^2}b} \). - Với \(a < 0\) và \(b \ge 0\), ta có: \(a\sqrt b = - \sqrt {{a^2}b} \). |
Ví dụ:
\(2\sqrt {\frac{1}{2}} = \sqrt {{2^2}.\frac{1}{2}} = \sqrt 2 \);
\(4\sqrt {\frac{7}{4}} - \sqrt {28} = \sqrt {{4^2}.\frac{7}{4}} - \sqrt {28} = \sqrt {4.7} - \sqrt {28} = \sqrt {28} - \sqrt {28} = 0\).