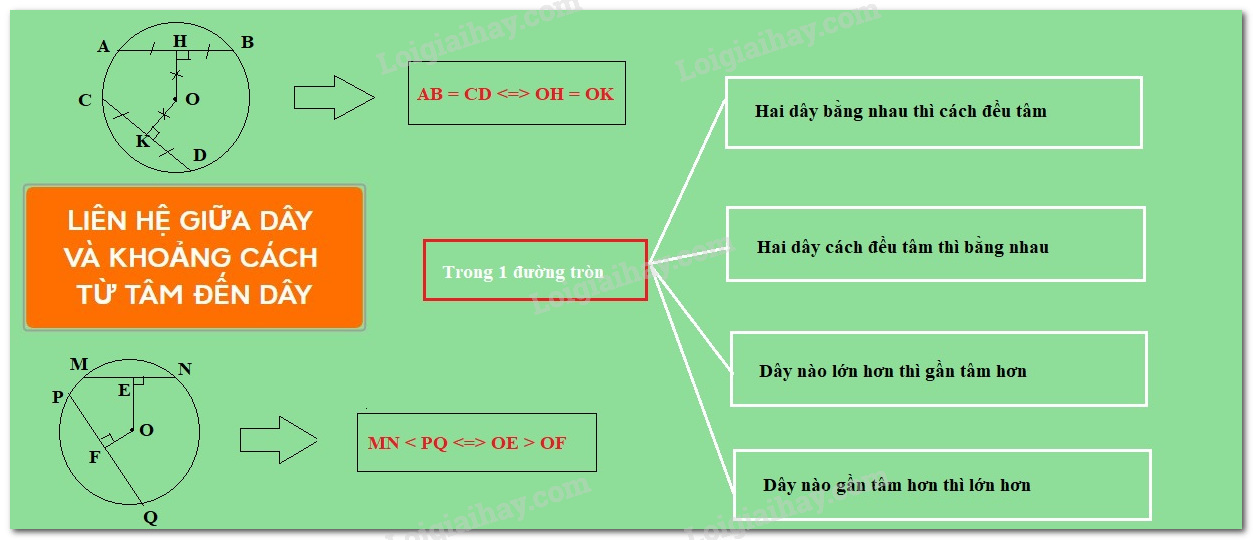
Lý thuyết liên hệ giữa dây và khoảng cách từ tâm đến dây
Trong một đường tròn: Hai dây bằng nhau thì cách đều tâm. Hai dây cách đều tâm thì bằng nhau.
Liên hệ giữa dây và khoảng cách từ tâm đến dây
Định lý 1: Trong một đường tròn:
a) Hai dây bằng nhau thì cách đều tâm.
b) Hai dây cách đều tâm thì bằng nhau.
Định lý 2. Trong hai dây của một đường tròn:
a) Dây nào lớn hơn thì dây đó gần tâm hơn.
b) Dây nào gần tâm hơn thì dây đó lớn hơn.
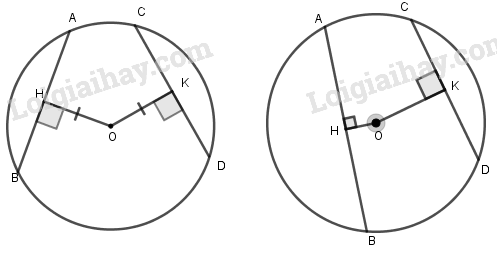
Xét đường tròn (O):
\(\begin{array}{l}OH \bot AB\left( {H \in AB} \right)\\OK \bot CD\left( {K \in CD} \right)\end{array}\)
Khi đó:
\(\begin{array}{l}AB = CD \Leftrightarrow OH = OK\\AB > CD \Leftrightarrow OH < OK\end{array}\)
CÁC DẠNG TOÁN THƯỜNG GẶP
So sánh hai đoạn thẳng
Phương pháp:
Ta thường sử dụng các kiến thức sau:
- Trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm.
+ Hai dây cách đều tâm thì bằng nhau.
- Trong hai dây của một đường tròn:
+ Dây nào lớn hơn thì dây đó gần tâm hơn.
+ Dây nào gần tâm hơn thì dây đó lớn hơn,
- Chứng minh hai tam giác bằng nhau, quan hệ giữa các yếu tố trong tam giác.