Lý thuyết tứ giác nội tiếp
Định nghĩa tứ giác nội tiếp
1. Các kiến thức cần nhớ
a. Định nghĩa tứ giác nội tiếp
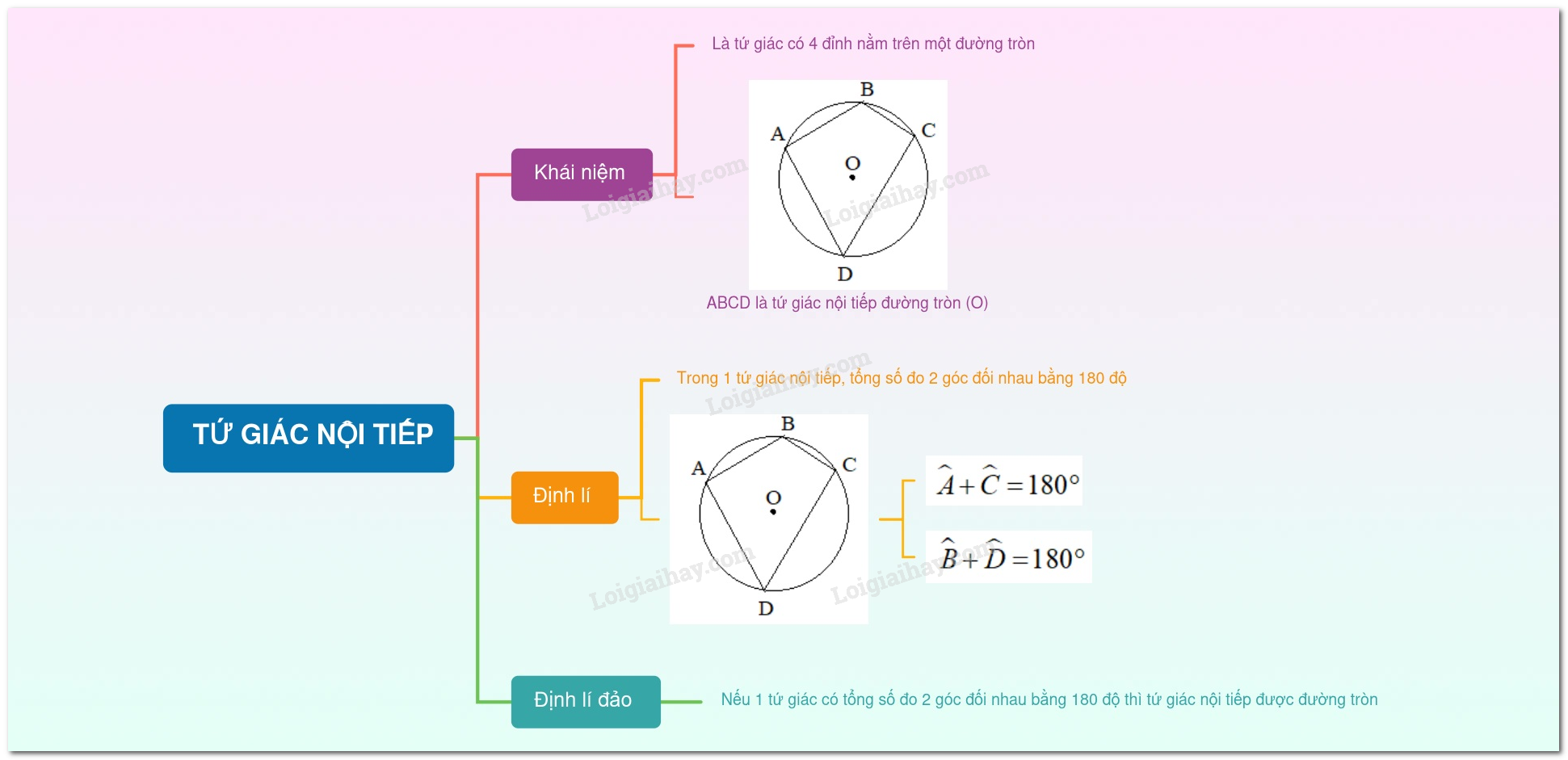
Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn đó.
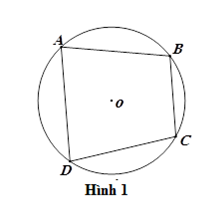
Ví dụ: Trong Hình $1$ , tứ giác \(ABCD\) nội tiếp \(\left( O \right)\) và \(\left( O \right)\) ngoại tiếp tứ giác \(ABCD.\)
Định lý
- Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng \(180^\circ \).
- Nếu một tứ giác có tổng số đo hai góc đối diện bằng \(180^\circ \) thì tứ giác đó nội tiếp được đường tròn.
Ví dụ: Trong hình \(1\) , tứ giác nội tiếp\(ABCD\) có \(\widehat A + \widehat C = 180^\circ ;\widehat B + \widehat D = 180^\circ \).
Một số dấu hiệu nhận biết tứ giác nội tiếp
- Tứ giác có tổng hai góc đối bằng \(180^\circ \).
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó.
- Tứ giác có bốn đỉnh cách đều một điểm (mà có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc \(\alpha \).
Chú ý : Trong các hình đã học thì hình chữ nhật, hình vuông, hình thang cân nội tiếp được đường tròn.
2. Các dạng toán thường gặp
Dạng 1: Chứng minh tứ giác nội tiếp
Phương pháp:
Để chứng minh tứ giác nội tiếp, ta có thể sử dụng một trong các cách sau :
Cách 1. Chứng minh tứ giác có tổng hai góc đối bằng \(180^\circ \).
Cách 2. Chúng minh tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc \(\alpha \).
Cách 3. Chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó.
Cách 4. Tìm được một điểm cách đều bốn đỉnh của tứ giác.
Dạng 2: Chứng minh các góc bằng nhau, đoạn thẳng bằng nhau, các đường thẳng song song, hệ thức giữa các cạnh…
Phương pháp:
Sử dụng tính chất của tứ giác nội tiếp.