Lý thuyết liên hệ giữa phép nhân và phép khai phương — Không quảng cáo

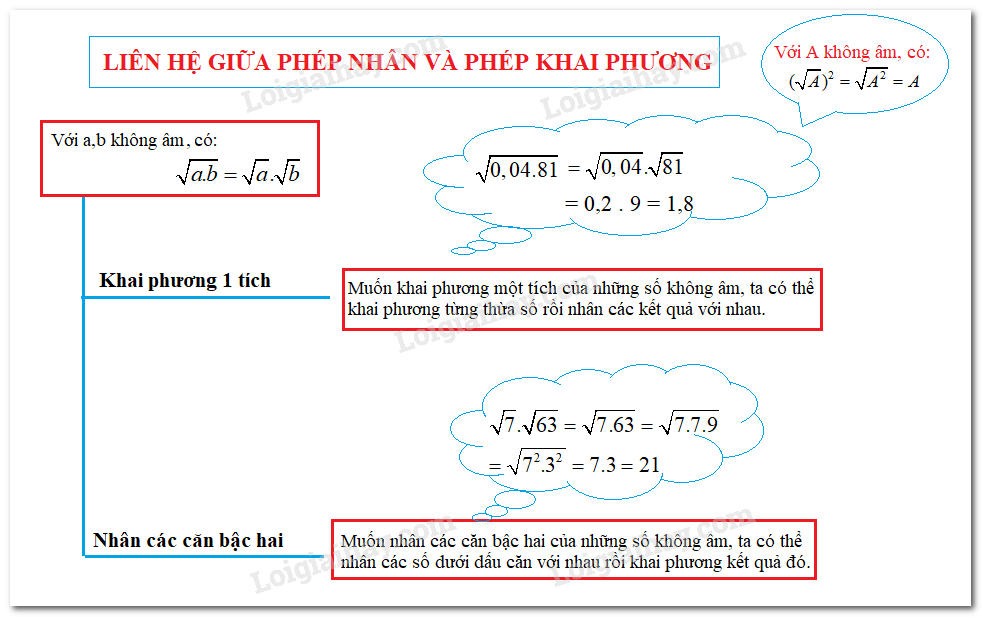
1. Định lí

Với các số \(a\) và \(b\) không âm ta có: \( \sqrt{a.b}=\sqrt a. \sqrt b\)

Lưu ý:

+) Với hai biểu thức không âm A và B, ta cũng có: \( \sqrt{A.B}=\sqrt A. \sqrt B\)

+) Nếu không có điều kiện A và B không âm thì không thể viết đẳng thức trên.

Chẳng hạn \( \sqrt{(-9).(-4)}\) được xác định nhưng đẳng thức \(\sqrt {(-9)}. \sqrt {(-4)}\) không xác định.

2. Áp dụng

a. Quy tắc khai phương một tích

Muốn khai phương một tích của những số không âm, ta có thể khai phương từng thừa số rồi nhân các kết quả với nhau.

+ Mở rộng: Với các số \(a, b,c\) không âm ta có: \( \sqrt{a.b.c}=\sqrt a. \sqrt b.\sqrt c \)

b. Quy tắc nhân các căn bậc hai

Muốn nhân các căn bậc hai của những số không âm, ta có thể nhân các số dưới dấu căn với nhau rồi khai phương kết quả đó.

+ Mở rộng: Với các số \(a, b,c\) không âm ta có: \( \sqrt a. \sqrt b .\sqrt c=\sqrt{a.b.c}\).

+ Với biểu thức \(A\) không âm, ta có: \({\left( {\sqrt A } \right)^2} = \sqrt {{A^2}}  = A\)

3. Dạng toán cơ bản

Dạng 1: Thực hiện phép tính

Sử dụng: Với hai biểu thức không âm A và B, ta có: \( \sqrt{A.B}=\sqrt A. \sqrt B\)

Ví dụ: \(\sqrt {32}  + \sqrt 8  = \sqrt {16.2}  + \sqrt {4.2} \)\( = \sqrt {16} .\sqrt 2  + \sqrt 4 .\sqrt 2 \)\( = 4\sqrt 2  + 2\sqrt 2  = 6\sqrt 2 \)

Dạng 2: Rút gọn biểu thức

Sử dụng: Với hai biểu thức không âm A và B, ta có: \( \sqrt{A.B}=\sqrt A. \sqrt B\)

Ví dụ:

\(\begin{array}{l} \sqrt {9\left( {{x^2} - 2x + 1} \right)} = \sqrt 9 .\sqrt {{x^2} - 2x + 1} \\ = 3.\sqrt {{{\left( {x - 1} \right)}^2}} = 3\left| {x - 1} \right| \end{array}\)