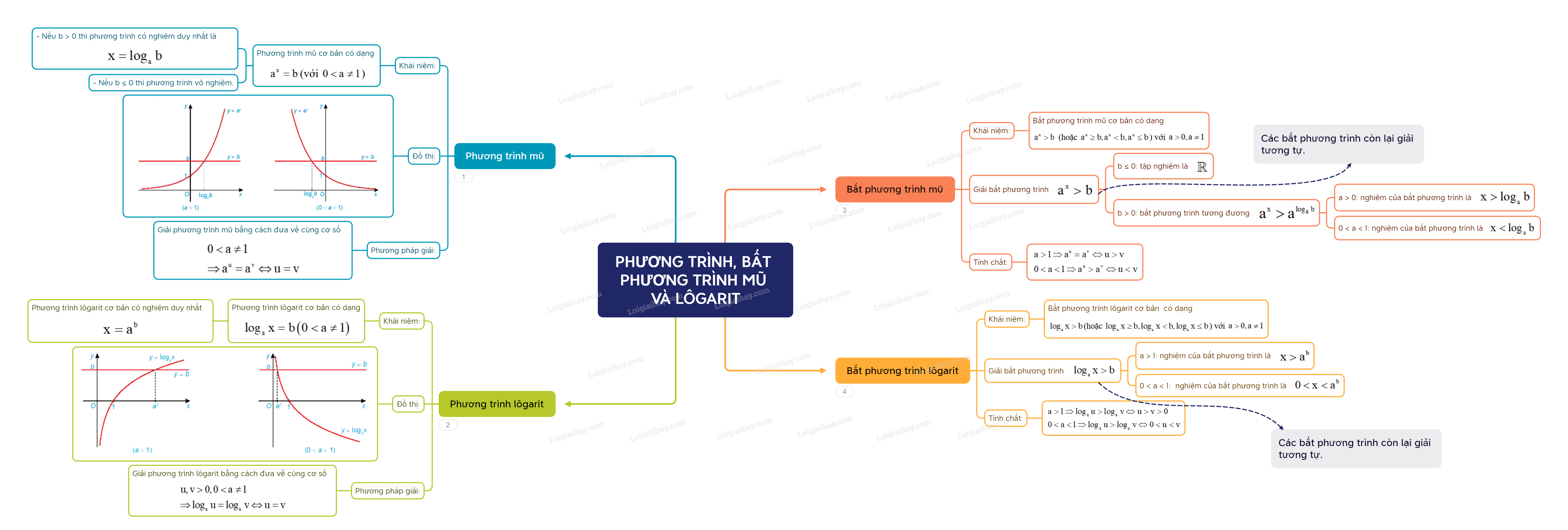
Lý thuyết Phương trình, bất phương trình mũ và lôgarit - Toán 11 Kết nối tri thức
1. Phương trình mũ
1. Phương trình mũ
Phương trình mũ cơ bản có dạng \({a^x} = b\)(với \(0 < a \ne 1\)).
- Nếu b > 0 thì phương trình có nghiệm duy nhất \(x = {\log _a}b\).
- Nếu b \( \le \) 0 thì phương trình vô nghiệm.
Minh họa bằng đồ thị:
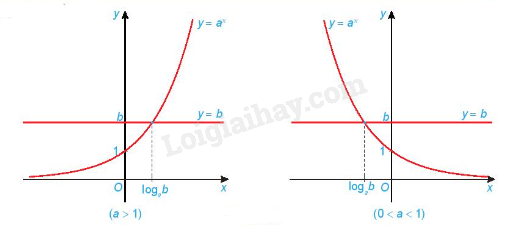
Chú ý: Phương pháp giải phương trình mũ bằng cách đưa về cùng cơ số:
Nếu \(0 < a \ne 1\) thì \({a^u} = {a^v} \Leftrightarrow u = v\).
2. Phương trình lôgarit
Phương trình lôgarit cơ bản có dạng \({\log _a}x = b\left( {0 < a \ne 1} \right)\).
Phương trình lôgarit cơ bản \({\log _a}x = b\) có nghiệm duy nhất \(x = {a^b}\).
Minh họa bằng đồ thị:
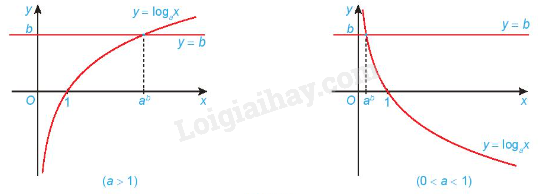
Chú ý: Phương pháp giải phương trình lôgarit bằng cách đưa về cùng cơ số:
Nếu \(u,v > 0\) và \(0 < a \ne 1\) thì \({\log _a}u = {\log _a}v \Leftrightarrow u = v\).
3. Bất phương trình mũ
Bất phương trình mũ cơ bản có dạng \({a^x} > b\) (hoặc \({a^x} \ge b,{a^x} < b,{a^x} \le b\)) với \(a > 0,a \ne 1\).
Xét bất phương trình dạng \({a^x} > b\):
- Nếu \(b \le 0\) thì tập nghiệm của bất phương trình là \(\mathbb{R}\).
- Nếu b > 0 thì bất phương trình tương đương với \({a^x} > {a^{{{\log }_a}b}}\).
Với a > 1, nghiệm của bất phương trình là \(x > {\log _a}b\).
Với \(0 < a < 1\), nghiệm của bất phương trình là \(x < {\log _a}b\).
Chú ý:
a) Các bất phương trình mũ cơ bản còn lại được giải tương tự.
b) Nếu a > 1 thì \({a^u} > {a^v} \Leftrightarrow u > v\).
Nếu 0 < a < 1 thì \({a^u} > {a^v} \Leftrightarrow u < v\).
4. Bất phương trình lôgarit
Bất phương trình lôgarit cơ bản có dạng \({\log _a}x > b\)(hoặc \({\log _a}x \ge b,{\log _a}x < b,{\log _a}x \le b\)) với \(a > 0,a \ne 1\).
Xét bất phương trình dạng \({\log _a}x > b\):
- Nếu a > 1 thì nghiệm của bất phương trình là \(x > {a^b}\).
- Nếu 0 < a < 1 thì nghiệm của bất phương trình là \(0 < x < {a^b}\).
Chú ý:
a) Các bất phương trình lôgarit cơ bản còn lại được giải tương tự.
b) Nếu a > 1 thì \({\log _a}u > {\log _a}v \Leftrightarrow u > v > 0\).
Nếu 0 < a < 1 thì \({\log _a}u > {\log _a}v \Leftrightarrow 0 < u < v\).