Lý thuyết về căn thức bậc hai và hằng đẳng thức √A^2= |A|
Lý thuyết về căn thức bậc hai và hằng đẳng thức √A^2= |A|. Với A là một biểu thức đại số, người ta goi·
1. Căn thức bậc hai
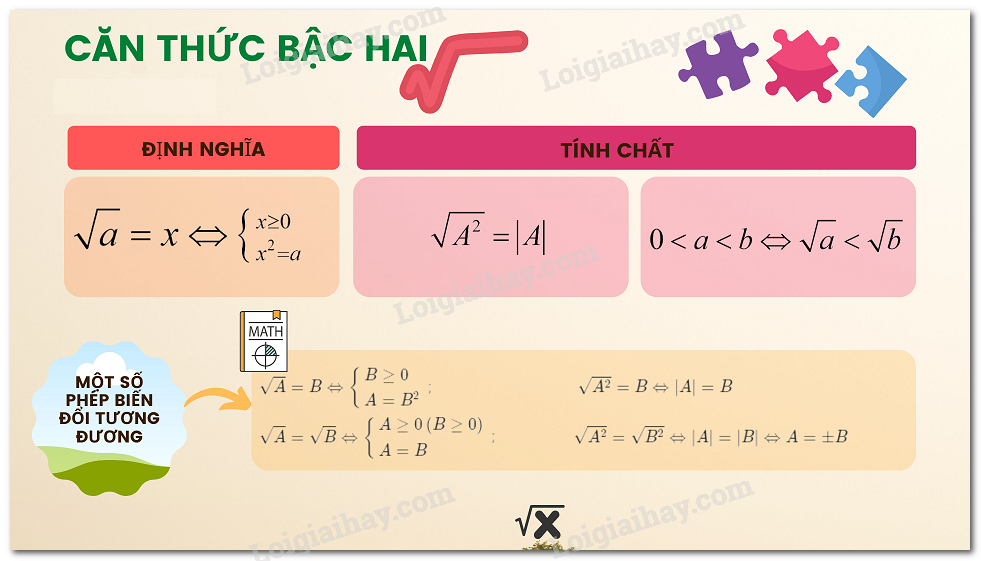
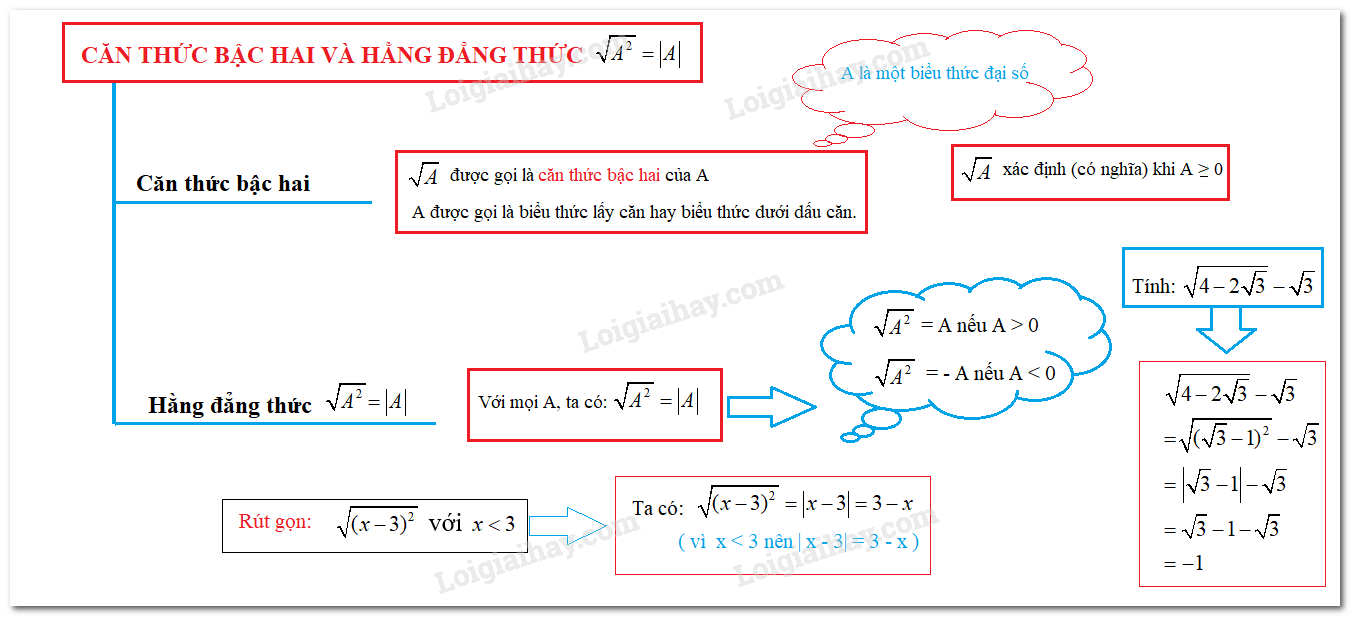
Với \(A\) là một biểu thức đại số, người ta gọi \(\sqrt A \) là căn thức bậc hai của \(A\). Khi đó, \(A\) được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.
\(\sqrt A \) xác định hay có nghĩa khi \(A\) lấy giá trị không âm.
2. Hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\)
Với mọi số \(a\), ta có \(\sqrt {{a^2}} = \left| a \right|\).
* Một cách tổng quát, với \(A\) là một biểu thức ta có
\(\sqrt {{A^2}} = \left| A \right|\) nghĩa là
\(\sqrt {{A^2}} = A\) nếu \(A \ge 0\) và \(\sqrt {{A^2}} = - A\) nếu \(A < 0\).
3. Các dạng toán cơ bản
Dạng 1: Tìm điều kiện để căn thức xác định
Ta có \(\sqrt A \) xác định hay có nghĩa khi \(A\ge 0\)
Ví dụ: \(\sqrt {x - 1} \) xác định khi \(x - 1 \ge 0 \Leftrightarrow x \ge 1\)
Dạng 2: Rút gọn biểu thức
Sử dụng: Với \(A\) là một biểu thức ta có \(\sqrt {{A^2}} = \left| A \right|\)
Vì dụ: Với \(x>2\) ta có: \(A = \dfrac{{\sqrt {{x^2} - 4x + 4} }}{{x - 2}}\)\( = \dfrac{{\sqrt {{{\left( {x - 2} \right)}^2}} }}{{x - 2}} = \dfrac{{\left| {x - 2} \right|}}{{x - 2}} \)\(= \dfrac{{x - 2}}{{x - 2}} = 1\)