Lý thuyết về dấu hiệu nhận biết tiếp tuyến của đường tròn
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
1. Các kiến thức cần nhớ
a) Tính chất của tiếp tuyến
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
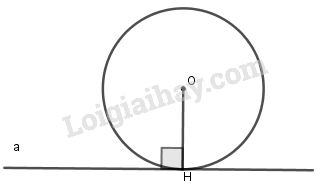
Trong hình trên a là tiếp tuyến của đường tròn \((O).\)
\(\Rightarrow a\perp OH\) tại \(H\) (với H là tiếp điểm).
b) Dấu hiệu nhận biết tiếp tuyến của đường tròn
Định lý: Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
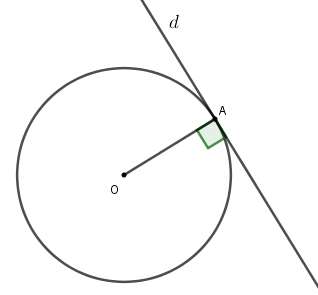
Ngoài ra, nhắc lại một số dấu hiệu đã biết:
+) Nếu một đường thằng và một đường tròn chỉ có một điểm chung thì đường thẳng đó là tiếp tuyến của đường tròn.
+) Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
2. Các dạng toán thường gặp
Dạng 1: Chứng minh một đường thẳng là tiếp tuyến của đường tròn
Phương pháp:
Để chứng minh đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm là $A$, ta có thể làm theo cách sau:
Cách 1. Chứng minh $OA \bot d$ tại $A$ và $A \in \left( O \right)$.
Cách 2. Vẽ $OH \bot d$. Chứng minh $OH \equiv OA = R$.
Cách 3. Vẽ tiếp tuyến $d'$ của $\left( O \right)$. Ta chứng minh $d \equiv d'$.
Dạng 2: Bài toán tính độ dài
Phương pháp:
Vận dụng định lý về tiếp tuyến và hệ thức lượng trong tam giác vuông để tính toán.