Bài 10 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho hình chóp \(S.ABCD\) với \(ABCD\) là hình thoi cạnh \(a\), tam giác \(SA{\rm{D}}\) đều. \(M\) là điểm trên cạnh \(AB\), \(\left( \alpha \right)\) là mặt phẳng qua \(M\) và \(\left( \alpha \right)\parallel \left( {SAD} \right)\) cắt \(CD,SC,SB\) lần lượt tại \(N,P,Q\).
Đề bài
Cho hình chóp \(S.ABCD\) với \(ABCD\) là hình thoi cạnh \(a\), tam giác \(SA{\rm{D}}\) đều. \(M\) là điểm trên cạnh \(AB\), \(\left( \alpha \right)\) là mặt phẳng qua \(M\) và \(\left( \alpha \right)\parallel \left( {SAD} \right)\) cắt \(CD,SC,SB\) lần lượt tại \(N,P,Q\).
a) Chứng minh rằng \(MNPQ\) là hình thang cân.
b) Đặt \(AM = x\), tính diện tích \(MNPQ\) theo \(a\) và \(x\).
Phương pháp giải - Xem chi tiết
Sử dụng các định lí:
‒ Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đổi một song song.
‒ Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.
Lời giải chi tiết
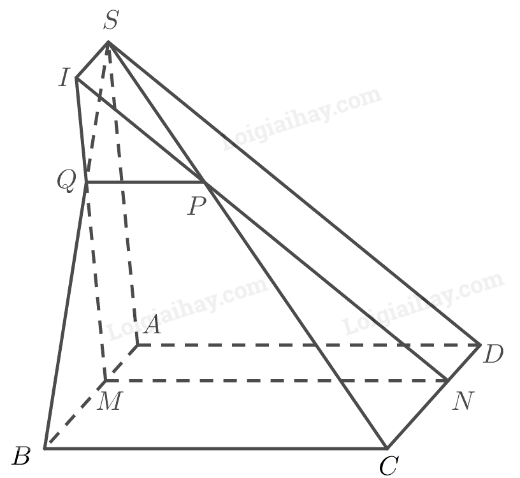
a) Ta có:
\(\left. \begin{array}{l}\left( \alpha \right) \cap \left( {SBC} \right) = PQ\\\left( \alpha \right) \cap \left( {ABCD} \right) = MN\\\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\end{array} \right\} \Rightarrow MN\parallel PQ\parallel BC\)
\( \Rightarrow MNPQ\) là hình thang (1).
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {SAB} \right) = MQ\\\left( {SA{\rm{D}}} \right) \cap \left( {SAB} \right) = SA\end{array} \right\} \Rightarrow MQ\parallel SA \Rightarrow \frac{{MQ}}{{SA}} = \frac{{BM}}{{AB}}\)
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {SC{\rm{D}}} \right) = NP\\\left( {SA{\rm{D}}} \right) \cap \left( {SC{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow NP\parallel SD \Rightarrow \frac{{NP}}{{SD}} = \frac{{CN}}{{C{\rm{D}}}}\)
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = AD\end{array} \right\} \Rightarrow MN\parallel AD\parallel BC \Rightarrow \frac{{BM}}{{AB}} = \frac{{CN}}{{C{\rm{D}}}}\)
\( \Rightarrow \frac{{MQ}}{{SA}} = \frac{{NP}}{{S{\rm{D}}}}\)
Mà tam giác \(SAD\) đều nên \(SA = S{\rm{D}}\)
\( \Rightarrow MQ = NP\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow MNPQ\) là hình thang cân.
b) Gọi \(I = MQ \cap NP\). Ta có:
\(\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {SA{\rm{D}}} \right) = SI\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SC{\rm{D}}} \right) \cap \left( {ABCD} \right) = C{\rm{D}}\end{array} \right\} \Rightarrow SI\parallel AB\parallel C{\rm{D}}\)
\(SI\parallel N{\rm{D}},S{\rm{D}}\parallel NI \Rightarrow SIN{\rm{D}}\) là hình bình hành \( \Rightarrow S{\rm{D}} = NI\)
\(SI\parallel MA,S{\rm{A}}\parallel MI \Rightarrow SIMA\) là hình bình hành \( \Rightarrow S{\rm{A}} = MI\)
Xét tam giác \(IMN\) và tam giác \(SAD\) có: \(MN\parallel A{\rm{D,}}MI\parallel SA,NI\parallel S{\rm{D}},MN = A{\rm{D}}\)
tam giác \(IMN\) là tam giác đều cạnh \(a\).
\(\begin{array}{l}SI\parallel AB \Rightarrow \frac{{SI}}{{BM}} = \frac{{IQ}}{{QM}} \Leftrightarrow \frac{{SI}}{{BM + SI}} = \frac{{IQ}}{{QM + IQ}} \Leftrightarrow \frac{{SI}}{{BM + MA}} = \frac{{IQ}}{{QM + IQ}}\\ \Leftrightarrow \frac{{SI}}{{AB}} = \frac{{IQ}}{{MI}} \Leftrightarrow IQ = \frac{{SI.MI}}{{AB}} = \frac{{x.a}}{a} = x\end{array}\)
\({S_{IMN}} = \frac{{{a^2}\sqrt 3 }}{4},{S_{IPQ}} = \frac{{{x^2}\sqrt 3 }}{4} \Rightarrow {S_{MNPQ}} = {S_{IMN}} - {S_{IPQ}} = \frac{{{a^2}\sqrt 3 }}{4} - \frac{{{x^2}\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{4}\left( {{a^2} - {x^2}} \right)\)