Bài 25 trang 111 SGK Toán 9 tập 1
Cho đường tròn tâm O có bán kính OA=R, dây BC vuông góc với OA tại trung điểm M của OA.
Đề bài
Cho đường tròn tâm \(O\) có bán kính \(OA=R\), dây \(BC\) vuông góc với \(OA\) tại trung điểm \(M\) của \(OA\).
a) Từ giác \(OCAB\) là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại \(B\), nó cắt đường thẳng \(OA\) tại \(E\). Tính độ dài \(BE\) theo \(R\).
Phương pháp giải - Xem chi tiết
a) +) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo vuông góc là hình thoi.
b) Hệ thức lượng giữa cạnh và góc trong tam giác vuông: \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\) thì \(AB=AC. \tan C.\)
Lời giải chi tiết
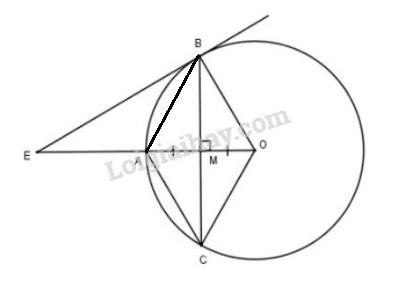
a) Xét đường tròn (O) có OA là 1 phần đường kính và BC là dây của đường tròn mà \(OA\perp BC\Rightarrow MB=MC\) (Theo định lý 2 - trang 103).
Mà \(M\) là trung điểm của OA.
\(\Rightarrow\) Tứ giác \(ABOC\) là hình bình hành ( tứ giác có 2 đường chéo OA và BC cắt nhau tại trung điểm M mỗi đường)
Mặt khác, \(BC \bot AO\)
Do đó \(ABOC\) là hình thoi (hình bình hành có hai đường chéo vuông góc).
b) Ta có \(ABOC\) là hình thoi nên \(BA=BO\) (tính chất)
Mà \(BO=OA=R\)
\(\Rightarrow\) \(OB=OA=BA\). Do đó tam giác \(ABO\) đều (Dấu hiệu nhận biết)
\(\Rightarrow \widehat{BOA}=60^{\circ}\) (Tính chất tam giác đều)
Ta có \(EB\) là tiếp tuyến của \((O)\) tại \(B\) \(\Rightarrow EB\perp OB\) hay \(\widehat{EBO}=90^o\).
Xét tam giác \(BOE\) vuông tại \(B\), áp dụng hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
\(BE=BO. \tan 60^{\circ}= R. \tan 60^0=R\sqrt{3}.\)