Bài 29 trang 79 SGK Toán 9 tập 2
Cho hai đường tròn (O) và (O') cắt nhau tại A và B
Đề bài
Cho hai đường tròn \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B\). Tiếp tuyến kẻ từ \(A\) đối với đường tròn (O') cắt (O) tại \(C\) đối với đường tròn \((O)\) cắt \((O')\) tại \(D\).
Chứng minh rằng \(\widehat {CBA} = \widehat {DBA}\).
Phương pháp giải - Xem chi tiết
+) Trong một đường tròn, góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì có số đo bằng nhau và bằng nửa số đo cung bị chắn.
+) Chỉ ra hai tam giác \(ABD\) và \(CBA\) đồng dạng để suy ra hai góc bằng nhau.
Lời giải chi tiết
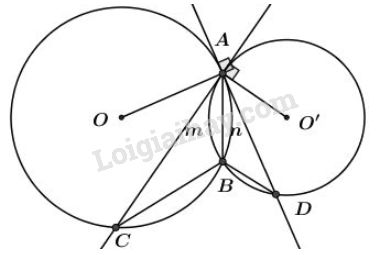
Xét đường tròn \( (O')\) có \(\widehat {ADB}\) là góc nội tiếp chắn cung \(\overparen{AmB}\)
\(\widehat {CAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(\overparen{AmB}\)
\(\Rightarrow\) \(\widehat {ADB} = \widehat {CAB}\) (1)
Xét đường tròn \((O)\) có \(\widehat {ACB}\) là góc nội tiếp chắn cung \(\overparen{AnB}\)
\(\widehat{BAD}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(\overparen{AnB}\)
\(\Rightarrow\) \(\widehat {ACB} = \widehat {BAD}\) (2)
Xét tam giác \(ABD\) và \(CBA\) có:
\(\widehat {CAB} = \widehat {ADB}\) (theo (1))
\(\widehat {ACB} = \widehat {BAD}\) (theo (2))
nên \(\Delta ACB \backsim \Delta DAB\left( {g - g} \right) \) suy ra \(\widehat {CBA} = \widehat {DBA}\) (hai góc tương ứng) (đpcm).