Bài 3 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh bằng $a\sqrt 2$, có các cạnh bên đều bằng $2a$.

a) Tính góc giữa $SC$ và $AB$.

b) Tính diện tích hình chiếu vuông góc của tam giác $SAB$ trên mặt phẳng $\left( {ABCD} \right)$.

Lời giải chi tiết

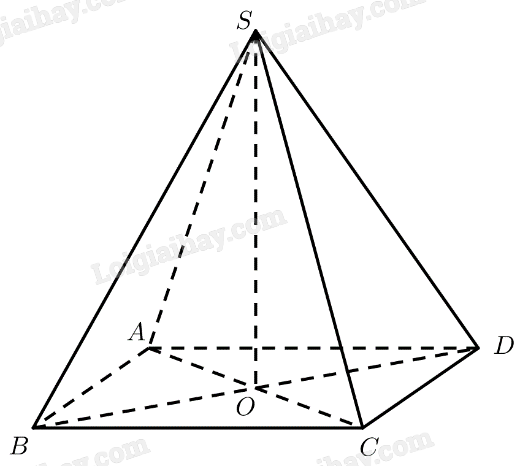
a) Ta có:

$AB\parallel C{\rm{D}} \Rightarrow \left( {SC,AB} \right) = \left( {SC,C{\rm{D}}} \right) = \widehat {SC{\rm{D}}}$

Xét $\Delta SCD$ có:

$\cos \widehat {SCD} = \frac{{S{C^2} + C{{\rm{D}}^2} - S{{\rm{D}}^2}}}{{2.SC.C{\rm{D}}}} = \frac{{\sqrt 2 }}{4} \Rightarrow \widehat {SCD} \approx {69^ \circ }18'$

Vậy $\left( {SC,AB} \right) \approx {69^ \circ }18'$.

b) Gọi $O = AC \cap B{\rm{D}}$.

$\Delta SAC$ cân tại $S \Rightarrow SO \bot AC$

$\Delta SB{\rm{D}}$ cân tại $S \Rightarrow SO \bot B{\rm{D}}$

$\Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow O$ là hình chiếu vuông góc của $S$ lên mặt phẳng $\left( {ABCD} \right)$.

Lại có $A,B \in \left( {ABCD} \right)$.

Vậy tam giác $OAB$ là hình chiếu vuông góc của tam giác $SAB$ lên mặt phẳng $\left( {ABCD} \right)$

Ta có: $AC = \sqrt {A{B^2} + B{C^2}}  = 2a$

Mà ABCD là hình vuông nên O là trung điểm của mỗi đường chéo.

$\begin{array}{l} \Rightarrow AO = BO = \frac{{AC}}{2} = a\\ \Rightarrow {S_{OAB}} = \frac{1}{2}AO.BO = \frac{1}{2}a.a = \frac{1}{2}{a^2}\end{array}$

Vậy diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD) là $\frac{1}{2}{a^2}$