Bài 33 trang 125 SGK Toán 9 tập 2
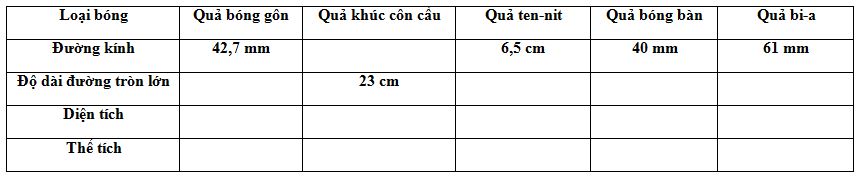
Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau (làm tròn kết quả đến chữ số thập phân thứ hai):
Đề bài
Dụng cụ thể thao
Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau (làm tròn kết quả đến chữ số thập phân thứ hai):
Phương pháp giải - Xem chi tiết
+) Đường tròn đường kính \(d\) có bán kính \(R=\frac{d}{2}.\)
+) Độ dài đường tròn lớn bán kính \(R\) là: \(C=2 \pi R = \pi d.\)
+) Diện tích mặt cầu bán kính \(R\) là: \(S=4 \pi R^2 = \pi d^2.\)
+) Thể tích hình cầu bán kính \(R\) là: \(V=\dfrac{4}{3} \pi R^3 =\dfrac{1}{6} \pi d^3 .\)
Lời giải chi tiết
Lấy \(\pi \approx 3,14\)
+ Quả bóng gôn: Khi \(d = 42,7mm = 4,27cm\), suy ra \(R \approx 2,14cm\)
- Độ dài đường tròn lớn \(C = \pi d \approx 13,41\left( {cm} \right).\)
- Diện tích \(S = \pi {d^2} = \pi .4,{27^2} \approx 57,25\left( {c{m^2}} \right)\)
- Thể tích \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}.3,14.{\left( {2,14} \right)^3}\)\( \approx 41,03c{m^3}\)
+ Quả khúc côn cầu: Khi \(C = 23cm \Rightarrow d = \dfrac{C}{\pi } \approx 7,32\left( {cm} \right)\) và \(R \approx 3,66\left( {cm} \right).\)
- Diện tích \(S = \pi {d^2} = 7,{32^2}.3,14 \approx 168,25\left( {c{m^2}} \right)\)
- Thể tích \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3} \cdot 3,14 \cdot 3,{66^3}\)\( \approx 205,26\left( {c{m^3}} \right).\)
+ Quả ten-nít: Khi \(d = 6,5cm\) \( \Rightarrow R = 3,25cm.\)
- Độ dài đường tròn lớn \(C = \pi d \approx 20,41\left( {cm} \right).\)
- Diện tích \(S = \pi {d^2} \approx \pi .6,{5^2} \approx 132,67\left( {c{m^2}} \right).\)
- Thể tích \(V = \dfrac{4}{3}\pi {R^3} \approx \dfrac{4}{3} \cdot 3,14 \cdot 3,{25^3}\)\( \approx 143,72\left( {c{m^3}} \right).\)
+ Quả bóng bàn: Khi \(d = 40mm = 4cm\) \( \Rightarrow R = 2cm.\)
- Độ dài đường tròn lớn \(C = \pi d \approx 12,56\left( {cm} \right).\)
- Diện tích \(S = \pi {d^2} \approx 3,{14.4^2} \approx 50,24\left( {c{m^2}} \right).\)
- Thể tích \(V = \dfrac{4}{3}\pi {R^3} \approx \dfrac{4}{3} \cdot 3,14 \cdot {2^3}\)\( \approx 33,49\left( {c{m^3}} \right).\)
+ Quả bi-a: Khi \(d = 61mm = 6,1cm\), suy ra \(R = 3,05\left( {cm} \right).\)
- Độ dài đường tròn lớn \(C = \pi d \approx 19,15\left( {cm} \right).\)
- Diện tích \(S = \pi {d^2} \approx 3,14.6,{1^2} \approx 116,84\left( {c{m^2}} \right).\)
- Thể tích \(V = \dfrac{4}{3}\pi {R^3} \approx \dfrac{4}{3} \cdot 3,14 \cdot 3,{05^3}\)\( \approx 118,79\left( {c{m^3}} \right).\)
Điền kết quả vào bảng trên ta có :
