Bài 5 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạo
Một cái lều có dạng hình lăng trụ (ABC.A'B'C') có cạnh bên (AA')vuông góc với đáy (Hình 24).
Đề bài
Một cái lều có dạng hình lăng trụ \(ABC.A'B'C'\) có cạnh bên \(AA'\)vuông góc với đáy (Hình 24). Cho biết \(AB = AC = 2,4m;BC = 2{\rm{ }}m;AA' = 3m\).
a) Tính góc giữa hai đường thẳng \(AA'\) và \(BC\); \(A'B'\) và \(AC\).
b) Tính diện tích hình chiếu vuông góc của tam giác \(ABB'\) trên mặt phẳng \(\left( {BB'C'C} \right)\).
Phương pháp giải - Xem chi tiết
a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).
b) Sử dụng phép chiếu vuông góc.
Lời giải chi tiết
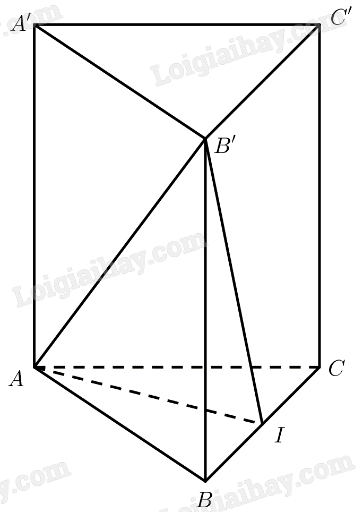
a) Ta có: \(AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot BC \Rightarrow \left( {AA',BC} \right) = {90^ \circ }\)
\(A'B'\parallel AB \Rightarrow \left( {A'B',AC} \right) = \left( {AB,AC} \right) = \widehat {BAC}\)
Xét tam giác \(ABC\) có:
\(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{47}}{{72}} \Rightarrow \widehat {BAC} \approx {49^ \circ }15'\)
Vậy \(\left( {A'B',AC} \right) \approx {49^ \circ }15'\).
b) Gọi \(I\) là trung điểm của \(BC\)
Tam giác \(ABC\) cân tại \(A \Rightarrow AI \bot BC\)
\(\left. \begin{array}{l}AA' \bot \left( {ABC} \right)\\BB'\parallel AA'\end{array} \right\} \Rightarrow BB' \bot \left( {ABC} \right) \Rightarrow BB' \bot AI\)
\( \Rightarrow AI \bot \left( {BB'C'C} \right)\)
\( \Rightarrow I\) là hình chiếu vuông góc của \(A\) trên mặt phẳng \(\left( {BB'C'C} \right)\)
Có \(B,B' \in \left( {BB'C'C} \right)\)
Vậy \(\Delta IBB'\) là hình chiếu vuông góc của \(\Delta ABB'\) trên mặt phẳng \(\left( {BB'C'C} \right)\)
Ta có: \(BB' = AA' = 3,BI = \frac{1}{2}BC = 1 \Rightarrow {S_{\Delta IBB'}} = \frac{1}{2}BB'.BI = 1,5\left( {{m^2}} \right)\)