Bài 5 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135°. Tính số mét khối đất cần phải di chuyển ra khỏi hầm.

Lời giải chi tiết

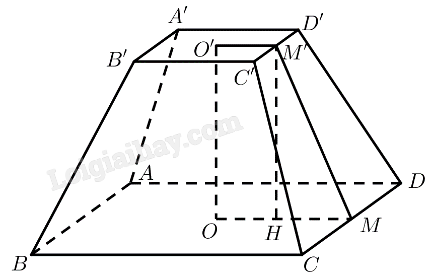
Mô hình hoá cái hầm bằng cụt chóp tứ giác đều $ABCD.A'B'C'D'$ với $O,O'$ là tâm của hai đáy. Vậy $AB = 14,A'B' = 10$.

Gọi $M,M'$ lần lượt là trung điểm của $CD,C'D'$.

$A'B'C'{\rm{D}}'$ là hình vuông $\Rightarrow O'M' \bot C'{\rm{D}}'$

$CDD'C'$ là hình thang cân $\Rightarrow MM' \bot C'D'$

Vậy $\widehat {MM'O'}$ là góc nhị diện giữa mặt bên và đáy nhỏ.

$\Rightarrow \widehat {MM'O'} = {135^ \circ } \Rightarrow \widehat {M'MO} = {180^ \circ } - \widehat {MM'O'} = {45^ \circ }$

Kẻ $M'H \bot OM\left( {H \in OM} \right)$

$OMM'O'$ là hình chữ nhật

$\Rightarrow OH = O'M' = 5,MH = OM - OH = 2,M'H = OO' = MH.\tan {45^ \circ } = 2$

Diện tích đáy lớn là: $S = A{B^2} = {14^2} = 196\left( {{m^2}} \right)$

Diện tích đáy bé là: $S' = A'B{'^2} = {10^2} = 100\left( {{m^2}} \right)$

Số mét khối đất cần phải di chuyển ra khỏi hầm là:

$V = \frac{1}{3}h\left( {S + \sqrt {SS'}  + S'} \right) = \frac{1}{3}.2\left( {196 + \sqrt {196.100}  + 100} \right) = \frac{{872}}{3} \approx 290,67\left( {{m^3}} \right)$