Bài 8 trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo
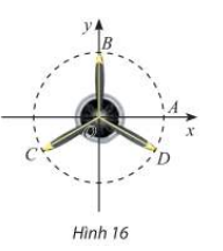
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?
Đề bài
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?
\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ, xác định góc lượng giác của điểm B, C, D.
Lời giải chi tiết
+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{{2\pi }}{3}\)
Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.
Với k = 2 thì \(\frac{\pi }{2} + 2.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.
+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{\pi }}{3} =\frac{5\pi }{6} \) không biểu diễn bởi điểm nào.
+ Xét góc lượng giác \(\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Với k = 1 thì \(\frac{{ - \pi }}{6}+ 1.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 2 thì \(\frac{{ - \pi }}{6}+ 2.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.
Với k = 3 thì \(\frac{{ - \pi }}{6} + 3.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.
Vậy các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác
\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\,\,\left( {k \in \mathbb{Z}} \right)\)