Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao
Từ đồ thị của hàm số y = sinx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó :
Từ đồ thị của hàm số \(y = \sin x\), hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó :
a. \(y = -\sin x\)
b. \(y = \left| {\sin x} \right|\)
c. \(y = \sin|x|\)
LG a
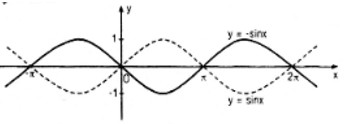
\(y = -\sin x\)
Lời giải chi tiết:
Đồ thị của hàm số \(y = -\sin x\) là hình đối xứng qua trục hoành của đồ thị hàm số \(y = \sin x\)
LG b
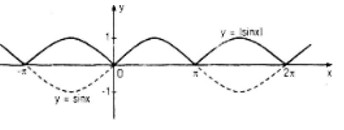
\(y = \left| {\sin x} \right|\)
Lời giải chi tiết:
Ta có: \(\left| {\sin x} \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,\sin x \ge 0} \cr { - \sin x\,\text{ nếu }\,\sin x < 0} \cr} } \right.\)
Do đó đồ thị của hàm số \(y = |\sin x|\) có được từ đồ thị \((C)\) của hàm số \(y = \sin x\) bằng cách:
- Giữ nguyên phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(y ≥ 0\) (tức nửa mặt phẳng bên trên trục hoành kể cả bờ \(Ox\)).
- Lấy hình đối xứng qua trục hoành của phần đồ thị \((C)\) nằm trong nửa mặt phẳng \(y < 0\) (tức là nửa mặt phẳng bên dưới trục hoành không kể bờ \(Ox\));
- Xóa phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(y < 0\).
- Đồ thị \(y = |\sin x|\) là đường liền nét trong hình dưới đây :
LG c
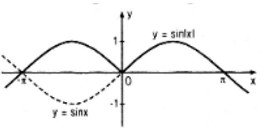
\(y = \sin|x|\)
Lời giải chi tiết:
Ta có: \(\sin \left| x \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,x \ge 0} \cr { - \sin x\,\text{ nếu }\,x < 0} \cr} } \right.\)
Do đó đồ thị của hàm số \(y = \sin|x|\) có được từ đồ thị \((C)\) của hàm số \(y = \sin x\) bằng cách :
- Giữ nguyên phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(x ≥ 0\) (tức nửa mặt phẳng bên phải trục tung kể cả bờ \(Oy\)).
- Xóa phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(x < 0\) (tức nửa mặt phẳng bên trái trục tung không kể bờ \(Oy\)).
- Lấy hình đối xứng qua trục tung của phần đồ thị \((C)\) nằm trong nửa mặt phẳng \(x > 0\)
- Đồ thị \(y = \sin|x|\) là đường nét liền trong hình dưới đây :