Câu 11 trang 106 SGK Đại số và Giải tích 11 Nâng cao
Cho hình vuông
Đề bài
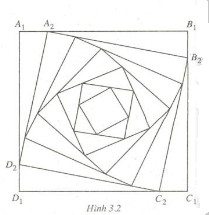
Cho hình vuông A 1 B 1 C 1 D 1 có các cạnh bằng 6cm. Người ta dựng các hình vuông A 2 B 2 C 2 D 2 , A 3 B 3 C 3 D 3 , …, A n B n C n D n , … theo cách sau : Với mỗi n = 2, 3, 4, … lấy các điểm A n , B n , C n , và D n tương ứng trên các cạnh A n-1 B n-1 , B n-1 C n-1 , C n-1 D n-1 và D n-1 A n-1 sao cho A n-1 A n = 1cm và A n B n C n D n là một hình vuông (h.3.2). Xét dãy số (u n ) với u n là độ dài cạnh của hình vuông A n B n C n D n .
Hãy cho dãy số (u n ) nói trên bởi hệ thức truy hồi.
Lời giải chi tiết
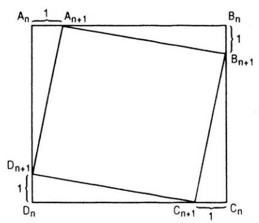
Với mỗi \(n \in \mathbb N^*\), xét các hình vuông \({A_n}{B_n}{C_n}{D_n}\) và \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}{D_{n + 1}},\) ta có
\(\eqalign{& {u_{n + 1}} = {A_{n + 1}}{B_{n + 1}} \cr&= \sqrt {{{\left( {{A_{n + 1}}{B_n}} \right)}^2} +{{\left( {{B_n}{B_{n + 1}}} \right)}^2}} \cr & = \sqrt {{{\left( {{A_n}{B_n} - 1} \right)}^2} + {1^2}} \cr & = \sqrt {{{\left( {{u_n} - 1} \right)}^2} + 1} \cr} \)