Câu 13 trang 18 SGK Hình học 11 Nâng cao
Cho hai tam giác vuông cân OAB
Đề bài
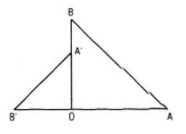
Cho hai tam giác vuông cân OAB và OA'B' có chung đỉnh O sao cho O nằm trên đoạn thẳng AB' và nằm ngoài đoạn thẳng A'B (h.16). Gọi G và G' lần lượt là trọng tâm các tam giác OAA' và OBB'.Chứng minh GOG' là tam giác vuông cân.
Lời giải chi tiết
Gọi Q là phép quay tâm O, góc quay \({\pi \over 2}\) (bằng góc lượng giác (OA ; OB)).
Khi đó Q:
+) biến O thành O
+) biến A thành B
+) biến A’ thành B’
Tức là Q biến tam giác OAA’ và OBB’
Bởi vậy Q biến G (trọng tâm tam giác OAA’) thành G’ (trọng tâm tam giác OBB’).
Suy ra \(OG = OG’\) và \(\widehat {GOG'} = {\pi \over 2}\)
Vậy GOG’ là tam giác vuông cân tại đỉnh O
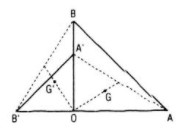
Chú ý: Phép quay Q biến trọng tâm G tam giác ABC thành trọng tâm G’ của tam giác A’B’C’ ảnh của △ABC qua Q được suy ra từ phép quay Q biến trung điểm của đoạn thẳng thành trung điểm đoạn thẳng.
Nghĩa là do phép quay Q biến AA' thành BB' thì biến trung điểm M của AA' thành trung điểm N của BB'.
Do đó Q biến OM thành ON. Khi đó Q biến G (thuộc OM) thành G' (thuộc ON) và \(OG' = OG = \frac{2}{3}OM = \frac{2}{3}ON\).
Vậy Q biến G thành G' là trọng tâm tam giác OBB'.