Câu 2 trang 124 SGK Hình học 11 Nâng cao
Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Kẻ MM’, NN’, PP’, QQ’ lần lượt vuông góc với CD, DA, AB, BC.
Đề bài
Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Kẻ MM’, NN’, PP’, QQ’ lần lượt vuông góc với CD, DA, AB, BC.
a. Gọi I là giao điểm của MP và NQ. Phép đối xứng tâm Đ I biến các đường thẳng MM’, NN’, PP’, QQ’ thành những đường thẳng nào ?
b. Chứng tỏ rằng bốn đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại một điểm. Nhận xét gì về vị trí điểm đồng quy và hai điểm I, O?
Lời giải chi tiết
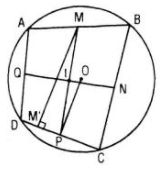
a. MNPQ là hình bình hành nên I là trung điểm
của MP và NQ.
Phép đối xứng tâm Đ I biến điểm M thành điểm P, biến đường thẳng MM’ thành đường thẳng đi qua P và song song với MM’, tức là vuông góc với DC.
Vậy đường thẳng MM’ được biến thành đường thẳng PO. Hoàn toàn tương tự : đường thẳng NN’ biến thành đường QO, đường thẳng PP’ biến thành đường MO, đường thẳng QQ’ biến thành đường NO.
b. Vì bốn đường thẳng MO, NO, PO, QO đồng quy tại điểm O nên bốn đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại O’ đối xứng với O qua điểm I.