Câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao
Trên tia Ox
Đề bài
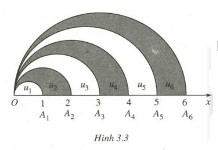
Trên tia Ox lấy các điểm A 1 , A 2 , …, A n , … sao cho với mỗi số nguyên dương n, OA n = n. Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính OA n , n = 1, 2, … . Kí hiệu u 1 là diện tích của nửa hình tròn đường kính OA 1 và với mỗi n ≥ 2, kí hiệu u n là diện tích của hình giới hạn bởi nửa đường tròn đường kính OA n – 1 , nửa đường tròn đường kính OA n và tia Ox (h 3.3). Chứng minh rằng dãy số (u n ) là một cấp số cộng. Hãy xác định công sai của cấp số cộng đó.
Lời giải chi tiết
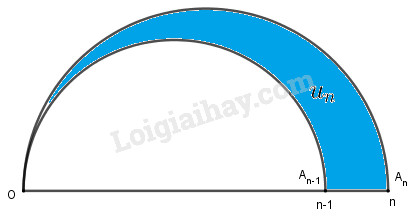
Với \(n ≥ 2\) ta có :
Diện tích nửa đường tròn đường kính \(OA_n\) là: \({S_n} = \frac{1}{2}\pi .{\left( {\frac{{O{A_n}}}{2}} \right)^2} = \frac{1}{8}\pi {n^2}\)
Diện tích nửa đường tròn đường kính \(OA_{n-1}\) là: \({S_{n-1}} = \frac{1}{2}\pi .{\left( {\frac{{O{A_{n-1}}}}{2}} \right)^2} = \frac{1}{8}\pi {(n-1)^2}\)
Do đó,
\(\eqalign{ & {u_n} ={S_n} - {S_{n-1}}\cr& = \frac{1}{8}\pi {n^2} - \frac{1}{8}\pi {\left( {n - 1} \right)^2} \cr & = {1 \over 8}\pi \left[ {\left( {{n^2} - {{\left( {n - 1} \right)}^2}} \right)} \right] \cr & = \frac{1}{8}\pi \left( {{n^2} - {n^2} + 2n - 1} \right)\cr&= {{\left( {2n - 1} \right)\pi } \over 8}\,\left( {n \ge 2} \right) \cr & \Rightarrow {u_{n + 1}} - {u_n} \cr&= {{2n + 1} \over 8}\pi - {{\left( {2n - 1} \right)} \over 8}\pi \cr&= {\pi \over 4},\forall n \ge 2 \cr} \)
Mặt khác
\({u_2} - {u_1} = {{3\pi } \over 8} - {\pi \over 8} = {\pi \over 4}\)
Vậy \({u_{n + 1}} - {u_n} = {\pi \over 4}\;\forall n \in\mathbb N^*\)
Do đó (u n ) là cấp số cộng với công sai \(d = {\pi \over 4}.\)