Câu 20 trang 143 SGK Đại số và Giải tích 11 Nâng cao — Không quảng cáo

Bông tuyết Vôn Kốc

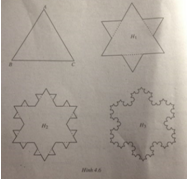
Ta bắt đầu từ một tam giác đều cạnh a. Chia mỗi cạnh của tam giác ABC thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài tam giác ABC rồi xóa đáy của nó, ta được đường gấp khúc khép kín H ₁ . Chia mỗi cạnh H ₁ thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài H ₁ rồi xóa đáy của nó, ta được đường gấp khúc khép kín H ₂ . Tiếp tục như vậy, ta được một hình giống như bông tuyết, gọi là bông tuyết Vôn Kốc (h. 4.6).

LG a

Gọi p ₁ , phương pháp, …, p _n , … là độ dài của H ₁ , H ₂ , …, H _n , … . Chứng minh rằng (p _n ) là một cấp số nhân. Tìm limp _n .

Giải chi tiết:

Số cạnh của H _n là 3.4 ⁿ .

Độ dài mỗi cạnh của H _n là  ${a \over {{3^n}}}$

Do đó độ dài của H­­ _n là  ${p_n} = {3.4^n}.{a \over {{3^n}}} = 3a{\left( {{4 \over 3}} \right)^n}$

Vậy dãy số (p _n ) là một cấp số nhân và  $\lim {p_n} = + \infty$

LG b

Gọi S _n là diện tích của miền giới hạn bởi đường gấp khúc H _n . Tính S _n và tìm giới hạn của dãy số (S _n ).

Hướng dẫn : Số cạnh của H _n là 3.4 ⁿ . Tìm độ dài mỗi cạnh của H _n , từ đó tính p _n . Để tính S _n cần chú ý rằng muốn có H _n+1 chỉ cần thêm vào một tam giác đều nhỏ trên mỗi cạnh của H _n .

Giải chi tiết:

Diện tích tam giác ABC cạnh a là  $S = {{{a^2}\sqrt 3 } \over 4}$

$\eqalign{ & {S_1} - S = 3.\left( {{S \over 9}} \right) = {S \over 3}, \cr & {S_2} - {S_1} = 4.3.\left( {{S \over {{9^2}}}} \right) = {S \over 3}.\left( {{4 \over 9}} \right) \cr & {S_3} - {S_2} = {4^2}.3.\left( {{S \over {{9^3}}}} \right) = {S \over 3}.{\left( {{4 \over 9}} \right)^2} \cr}$

Bằng phương pháp qui nạp, ta được :

${S_n} = {S_{n - 1}} = {4^{n - 1}}.3.\left( {{S \over {{9^n}}}} \right) = {S \over 3}.{\left( {{4 \over 9}} \right)^{n - 1}}$

Cộng từng vế n đẳng thức trên, ta được :

${S_n} - S = {S \over 3} + {S \over 3}.\left( {{4 \over 9}} \right) + {S \over 3}.{\left( {{4 \over 9}} \right)^2} + ... + {S \over 3}.{\left( {{4 \over 9}} \right)^{n - 1}}\,\,\left( 1 \right)$

Vế phải của (1) là tổng của n số hạng đầu tiên của cấp số nhân lùi vô hạn có số hạng đầu là ${S \over 3}$ và công bội là ${4 \over 9}$. Tổng của cấp số nhân này là :

$\left( {{S \over 3}} \right).{1 \over {1 - {4 \over 9}}} = {{3S} \over 5}$

Do đó  $\lim \left( {{S_n} - S} \right) = {{3S} \over 5}$

Suy ra  $\lim {S_n} = {{3S} \over 5} + S = {{8S} \over 5} = {8 \over 5}.{{{a^2}\sqrt 3 } \over 4} = {{2\sqrt 3 } \over 5}{a^2}$