Câu 33 trang 212 SGK Đại số và Giải tích 11 Nâng cao — Không quảng cáo

Tìm đạo hàm của mỗi hàm số sau :

LG a

$\displaystyle y = {{\sin x} \over x} + {x \over {{\mathop{\rm sinx}\nolimits} }}$

Phương pháp giải:

Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.

Giải chi tiết:

$y' = \dfrac{{\left( {\sin x} \right)'.x - \sin x.\left( {x'} \right)}}{{{x^2}}}$ $+ \dfrac{{x'\sin x - x.\left( {\sin x} \right)'}}{{{{\sin }^2}x}}$

$\eqalign{  & = {{x\cos x - \sin x} \over {{x^2}}} + {{\sin x - x\cos x} \over {{{\sin }^2}x}}  \cr  &  = \left( {x\cos x - {\mathop{\rm sinx}\nolimits} } \right)\left( {{1 \over {{x^2}}} - {1 \over {{{\sin }^2}x}}} \right) \cr}$

LG b

$\displaystyle y = {{{{\sin }^2}x} \over {1 + \tan 2x}}$

Phương pháp giải:

Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.

Giải chi tiết:

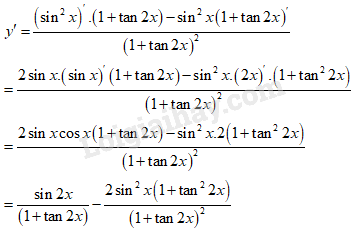
LG c

$y = \tan \left( {\sin x} \right)$

Phương pháp giải:

Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.

Giải chi tiết:

$y' = \left( {\sin x} \right)'.\dfrac{1}{{{{\cos }^2}\left( {\sin x} \right)}}$ $\displaystyle = {{\cos x} \over {{{\cos }^2}\left( {\sin x} \right)}}$

LG d

$y = x\cot \left( {{x^2} - 1} \right)$

Phương pháp giải:

Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.

Giải chi tiết:

$y' = x'.\cot \left( {{x^2} - 1} \right) + x.\left[ {\cot \left( {{x^2} - 1} \right)} \right]'$ $= \cot \left( {{x^2} - 1} \right) + x.\left( {{x^2} - 1} \right)'.\dfrac{{ - 1}}{{{{\sin }^2}\left( {{x^2} - 1} \right)}}$

$\eqalign{  & = \cot \left( {{x^2} - 1} \right) + x.{{ - 2x} \over {{{\sin }^2}\left( {{x^2} - 1} \right)}}  \cr  &  = \cot \left( {{x^2} - 1} \right) - {{2{x^2}} \over {{{\sin }^2}\left( {{x^2} - 1} \right)}} \cr}$

LG e

$\displaystyle y = {\cos ^2}\sqrt {{\pi  \over 4} - 2x}$

Phương pháp giải:

Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.

Giải chi tiết:

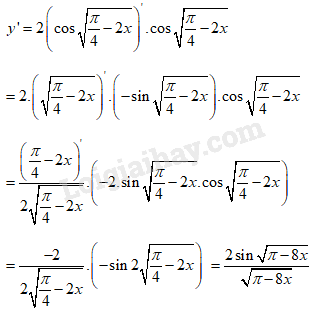
LG f

$y = x\sqrt {\sin 3x}$

Phương pháp giải:

Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.

Giải chi tiết:

$y' = x'\sqrt {\sin 3x}  + x.\left( {\sqrt {\sin 3x} } \right)'$ $= \sqrt {\sin 3x}  + x.\dfrac{{\left( {\sin 3x} \right)'}}{{2\sqrt {\sin 3x} }}$ $\displaystyle = \sqrt {\sin 3x}  + x.{{3\cos 3x} \over {2\sqrt {\sin 3x} }}$ $\displaystyle = {{2\sin 3x + 3x\cos 3x} \over {2\sqrt {\sin 3x} }}$