Đề kiểm tra 15 phút - Đề số 1 - Bài 4 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 4 - Chương 2 - Hình học 9
Đề bài
Cho nửa đường tròn (O), đường kính AB và một dây cung CD. Vẽ AP và BS vuông góc với CD. Chứng minh:
a. P và S ở bên ngoài đường tròn.
b. \(PC = DS\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Điểm A nằm ngoài đường tròn (O;R) nếu OA>R
Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
Lời giải chi tiết
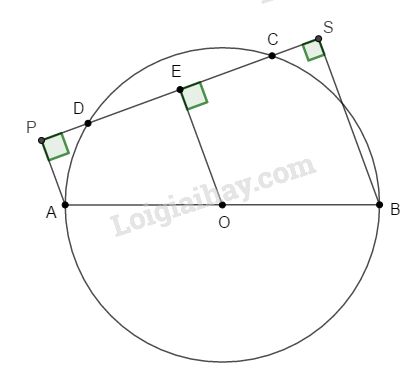
a. Ta có: AP // BS (⊥ CD) nên tứ giác APSB là hình thang vuông.
Kẻ \(OE ⊥ CD.\) Khi đó OE là đường trung bình của hình thang nên \(EP = ES.\)
Trong hình thang APSD có:
\(\widehat {OAP} + \widehat {OBS} = 180^\circ \)
và giả sử \(\widehat {OAP} \ge 90^\circ ,\)
Xét ∆PAO ta có: \(\widehat {PAO} > \widehat {APO} \Rightarrow OP > AO\)
mà AO là bán kính, do đó P nằm ngoài (O).
Mặt khác \(EP = ES\) (cmt)
\(⇒ SO = PO > OA\) nên S nằm ngoài (O)
b. Vì OE vuông góc với dây CD nên ta có: \(CE = DE\) (định lí đường kính dây cung)
mà \(EP = ES\) (cmt)
\(⇒ EP – CE = ES – DE\) hay \(PC = DS\).