Đề kiểm tra 15 phút - Đề số 1 - Bài 5 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 5 - Chương 2 - Hình học 9
Đề bài
Cho đường tròn (O), đường kính AB, tiếp tuyến tại điểm M thuộc (O) cắt hai tiếp tuyến tại A và B lần lượt tại C và D. Vẽ đường tròn tâm I có đường kính CD. Chứng minh AB tiếp xúc với đường tròn (I) tại O.
Phương pháp giải - Xem chi tiết
Sử dụng: Tính chất đường trung bình của hình thang
Chứng minh OI vuông góc với AB và bằng nửa CD
Lời giải chi tiết
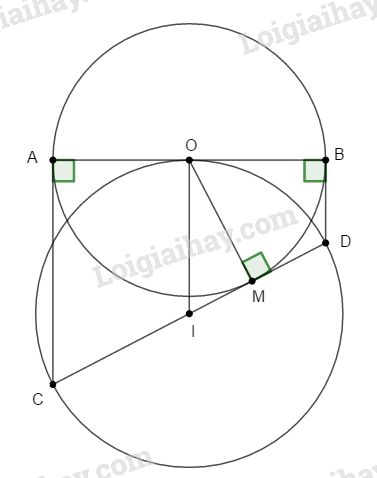
AC và BD là tiếp tuyến của (O) nên \(AC ⊥ AB\) và \(BD ⊥ AB ⇒ AC // BD\)
Do đó tứ giác ACDB là hình thang vuông, có O là trung điểm AB, I là trung điểm CD nên OI là đường trung bình của hình thang vuông. Vì vậy OI // AC.
\(⇒ OI ⊥ AB\) (1) và \(OI = {{AC + BD} \over 2}\)
Dễ dàng chứng minh \(∆OAC = ∆OMC ⇒ AC = MC\)
Tương tự : \(BD = MD \)\(\;\Rightarrow OI = {{MC + MD} \over 2} = {{CD} \over 2}\,\left( 2 \right)\)
Từ (1) và (2) chứng tỏ AB là tiếp tuyến của (I)