Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 2 - Hình học 9
Đề bài
Cho đường tròn (O) đường kính AB. Dây CD cắt đường kính AB tại điểm I. Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng : \(CH = DK.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
Trong một tam giác, đường thẳng đi qua trung điểm cạnh thứ nhất và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba của tam giác đó.
Lời giải chi tiết
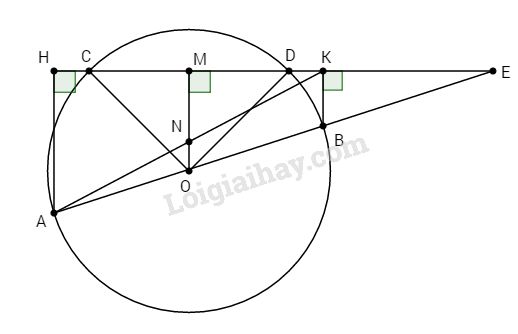
Kẻ \(OM ⊥ CD\), ta có: \(MC = MD\) (1) (định lí đường kính dây cung)
và OM // BK (cùng \(⊥ CD\))
Gọi N là giao điểm của OM và AK, ta có ON là đường trung bình của ∆ABK nên N là trung điểm của AK. Mặt khác trong tam giác vuông AHK ta có MN // AH nên MN là đường trung bình của ∆AHK.
Do đó M là trung điểm của HK
hay \(MH = MK\) (2)
Từ (1) và (2) \(⇒ MC – MH = MD – MK\) hay \(CH = DK\).