Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 3 - Hình học 9
Đề bài
Cho đường tròn (O) đường kính AB cố định. M là một điểm di động trên đường tròn. Nối MA, MB, trên tia đối của tia MA lấy điểm I sao cho MI = 2MB. Tìm tập hợp các điểm I.
Phương pháp giải - Xem chi tiết
+Phần thuận: Chứng minh I nằm trên cung chứa góc \(α\), vẽ trên đoạn AB.
+Phần đảo: Lấy một điểm I’ bất kì trên cung I 0 B I0B ( hoặc cung I 2 B I2B ) nối I’A cắt đường tròn (O) tại M’. Chứng minh \(M'I' = 2M'B.\)
+Kết luận
Lời giải chi tiết
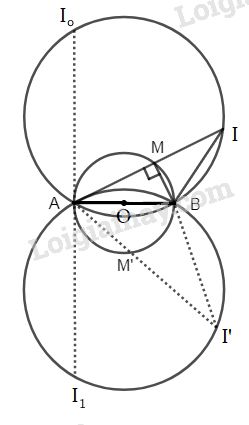
a) Phần thuận : Ta có \(\widehat {AMB} = 90^\circ \Rightarrow \widehat {BMI} = 90^\circ \)
Trong tam giác vuông IMB : \(\tan \widehat {AIB} =\dfrac {{BM}}{ {IM}} =\dfrac {1 }{ 2}\)
\( \Rightarrow \widehat {AIB} = \alpha \) không đổi \(\left( {\alpha \approx 24^\circ 34'} \right)\), AB cố định.
Vậy I nằm trên cung chứa góc \(α\), vẽ trên đoạn AB.
Giới hạn : I nằm trên hai cung \({I_0}B\) và \({I_1}B\) đối xứng nhau qua AB với \({I_0}{I_1} \bot AB\) tại A.
b) Phần đảo : Lấy một điểm I’ bất kì trên cung \({I_0}B\) ( hoặc cung \({I_2}B\) ) nối I’A cắt đường tròn (O) tại M’. Ta có \(\widehat {AM'B} = 90^\circ \). Do đó \(∆BM’I \) vuông. Khi đó :
\(\tan \widehat {BI'M} = \tan \alpha = \dfrac{{M'B}}{ {M'T'}} =\dfrac {1}{ 2}\)
\(\Rightarrow M'I' = 2M'B.\)
c) Kết luận : Tập hợp các điểm I là cung \({I_0}B\) và \({I_1}B\) đối xứng qua AB là phần của cung chứa góc α \(\left( {\tan \alpha = \dfrac{1 }{ 2}} \right)\) vẽ trên AB.