Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 9
Đề bài
Cho \(∆ABC\) vuông tại A, biết \({{AB} \over {AC}} = {2 \over 3},\) đường cao \(AH = 6cm\). Tính các cạnh của tam giác.
Phương pháp giải - Xem chi tiết
Sử dụng tam giác đồng dạng và hệ thức lượng trong tam giác vuông.
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\) và \(A{C^2} = CH.BC\)
+) \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
Lời giải chi tiết
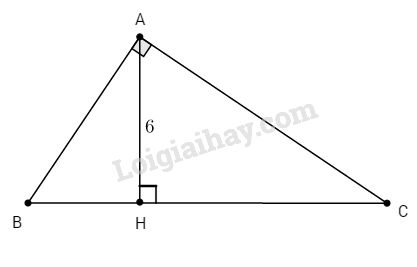
Ta có: \(∆AHB\) đồng dạng \(∆CHA\) (g.g) (vì có \(\widehat {BAH} = \widehat C\) (cùng phụ với \(\widehat B\) ))
\( \Rightarrow {{HA} \over {HC}} = {{AB} \over {AC}} = {2 \over 3} \)
\(\Rightarrow HC = {3 \over 2}HA = {3 \over 2}.6 = 9\,\left( {cm} \right)\) Tương tự: \({{HA} \over {HB}} = {{AC} \over {AB}} = {3 \over 2}\)
\(\Rightarrow HB = {2 \over 3}HA = {2 \over 3}.6 = 4\,\left( {cm} \right)\)
Do đó: \(BC = HB + HC = 4 + 9 = 13 (cm)\)
\(∆ABC\) vuông tại A, đường cao AH.
\( \Rightarrow A{B^2} = BC.BH\) (định lí 1)
\( \Rightarrow AB = \sqrt {BC.BH} = \sqrt {13.4} = 2\sqrt {13} \)\(\;(cm)\)
Tương tự, ta có:
\(AC = \sqrt {BC.CH} = \sqrt {13.9} = 3\sqrt {13} \)\(\,\left( {cm} \right)\)
Cách khác: Gọi cạnh huyền là a và hai cạnh góc vuông là b, c; đường cao là h.
Ta có: \({c \over b} = {2 \over 3} \Rightarrow b = {3 \over 2}c\)
Mặt khác ∆ABC vuông có h là đường cao:
\(\eqalign{ & {1 \over {{h^2}}} = {1 \over {{b^2}}} + {1 \over {{c^2}}}\cr&hay\,\,{1 \over {{6^2}}} = {1 \over {{{\left( {{3 \over 2}c} \right)}^2}}} + {1 \over {{c^2}}}\cr& \Leftrightarrow {1 \over {{6^2}}} = {4 \over {9{c^2}}} + {1 \over {{c^2}}} \cr & \Leftrightarrow {c^2} = 16 + 36\cr& \Leftrightarrow {c^2} = 52 \Leftrightarrow c = 2\sqrt {13} \,\left( {cm} \right) \cr} \)
Do đó \(b = {3 \over 2}.2\sqrt {13} = 3\sqrt {13} \,\left( {cm} \right)\)